Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Tam giác SAB đều và nằm trong một mặt phẳng vuông góc với đáy. Gọi H, K lần lượt là trung điểm của các cạnh AB và AD. Tính sin của góc t
33
22/05/2024
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Tam giác SAB đều và nằm trong một mặt phẳng vuông góc với đáy. Gọi H, K lần lượt là trung điểm của các cạnh AB và AD. Tính sin của góc tạo bởi giữa đường thẳng SA và mặt phẳng (SHK).
A. \(\frac{{\sqrt 2 }}{2}\);
B. \(\frac{{\sqrt 2 }}{4}\);
C. \(\frac{{\sqrt 7 }}{4}\);
D. \(\frac{{\sqrt {14} }}{4}\).
Trả lời
Lời giải
Đáp án đúng là: B.
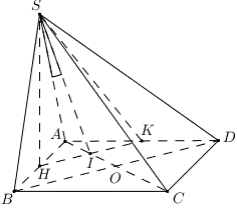
Theo đề bài ∆SAB đều nên SH ⊥ AB suy ra SH ⊥ (ABCD).
Gọi I = AC ∩ HK.
Do ABCD là hình vuông nên AC ⊥ BD.
Mà HK // BD (H là đường trung bình của \(\Delta ABD\) nên AC ⊥ HK.
Do đó AI ⊥ BD.
Ta có: \(\left\{ \begin{array}{l}AI \bot HK\\AI \bot SH(SH \bot (ABCD))\end{array} \right.\)\( \Rightarrow AI \bot (SHK)\).
Suy ra SI là hình chiếu của SA lên (SHK).
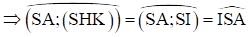
Gọi = AC ∩ BD, áp dụng định lí Ta-lét ta có:
\(\frac{{AI}}{{OA}} = \frac{{AH}}{{AB}} = \frac{1}{2} \Rightarrow AI = \frac{1}{2}OA = \frac{1}{2}AC = \frac{{a\sqrt 2 }}{4}\).
Xét ∆SIA vuông tại I ta có: \(\widehat {ISA} = \frac{{AI}}{{SA}} = \frac{{\frac{{a\sqrt 2 }}{4}}}{a} = \frac{{\sqrt 2 }}{4}\).
Vậy \[\sin \widehat {\left( {SA;\,\,\left( {SHK} \right)} \right)} = \frac{{\sqrt 2 }}{4}\].

