Lời giải
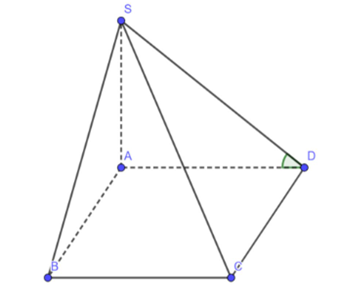
Vì ABCD là hình vuông nên CD ⊥ AD
Mà CD ⊥ SA (vì SA vuông góc với đáy ABCD)
Suy ra CD ⊥ (SAD)
Do đó CD ⊥ SD
Ta có (SCD) ∩ (ABCD) tại CD
Mà (SCD) có CD ⊥ SD, (ABCD) có CD ⊥ AD
Suy ra \(\widehat {((SC{\rm{D)}},(ABC{\rm{D}}))} = \widehat {(SD,A{\rm{D}})} = \widehat {SDA} = 60^\circ \)
Xét tam giác ASD vuông tại A có
\(\tan \widehat {S{\rm{D}}A} = \frac{{SA}}{{A{\rm{D}}}} \Leftrightarrow \tan 60^\circ = \frac{{SA}}{a}\)
Suy ra SA = a\(\sqrt 3 \)
Ta có VS.ABCD = \(\frac{1}{3}\). SA . SABCD = \(\frac{1}{3}\). a\(\sqrt 3 \) . a . a = \(\frac{{{a^3}}}{{\sqrt 3 }}\)
Vậy thể tích khối chóp S.ABCD bằng \(\frac{{{a^3}}}{{\sqrt 3 }}\).