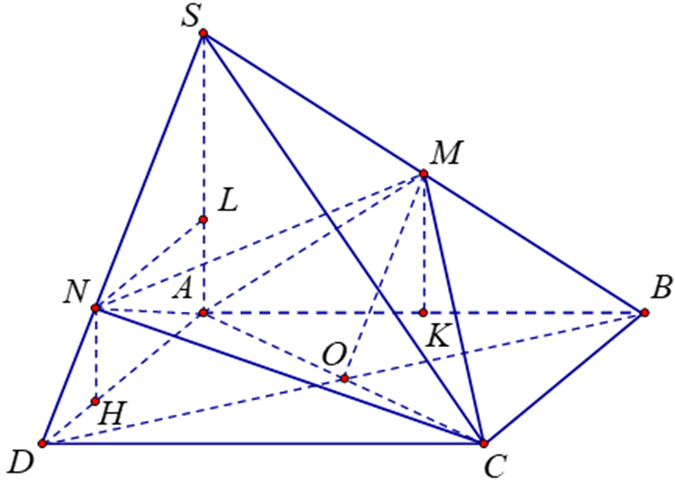
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA = a và SA vuông góc với đáy. Gọi M là trung điểm SB, N là điểm thuộc cạnh SD sao cho SN = 2ND. Tính thể tích V của khối tứ diện ACMN.
Ta có : VS.ABCD =\(\frac{1}{3}\)SABCD . SA=\(\frac{1}{3}\)∙ a2 ∙ a = \(\frac{{{a^3}}}{3}\)
\[\frac{{{V_{SAMN}}}}{{{V_{SABD}}}} = \frac{{SN}}{{SD}}\cdot\frac{{SM}}{{SB}} = .\frac{{23}}{{12}} = \frac{1}{3}\]
Mà \({V_{SABD}} = \frac{1}{2}{V_{SABCD}} = \frac{1}{2}\cdot\frac{{{a^3}}}{3} = \frac{{{a^3}}}{6}\)
\( \Rightarrow {V_{SAMN}} = \frac{{{a^3}}}{{18}}\)
Ta lại có :
\[\begin{array}{l}{V_{NADC}} = \frac{1}{3}\cdot{S_{ADC}}\cdotd(N;(ADC)) = \frac{1}{3}\cdot{S_{ADC}}\cdot\frac{1}{3}d(S;(ADC)) = \frac{1}{3}{V_{SABD}} = \frac{1}{6}{V_{SABCD}} = \frac{{{a^3}}}{{18}}\\{V_{MABC}} = \frac{1}{3}\cdot{S_{ABC}}\cdotd(M;(ABC)) = \frac{1}{3}\cdot{S_{ABC}}\cdot\frac{1}{2}d(S;(ABC)) = \frac{1}{2}{V_{SABC}} = \frac{1}{4}{V_{SABCD}} = \frac{{{a^3}}}{{12}}\end{array}\]
Mặt khác:
\[\begin{array}{l}{V_{C.SMN}} = \frac{1}{3}d(C,(SMN)).{S_{\Delta SMN}} = \frac{1}{3}d(A,(SMN)).{S_{\Delta SMN}} = \frac{{{a^3}}}{{18}}\\\end{array}\]
Vậy:
\({V_{ACMN}} = {V_{S.ABCD}} - {V_{NSAM}} - {V_{NADC}} - {V_{MABC}} - {V_{SCMN}} = \frac{{{a^3}}}{3} - \frac{{{a^3}}}{{18}} - \frac{{{a^3}}}{{18}} - \frac{{{a^3}}}{{12}} - \frac{{{a^3}}}{{18}} = \frac{{{a^3}}}{{12}}\).