Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. Tam giác SAB nằm trong mặt phẳng vuông góc với mặt phẳng (ABCD). Biết rằng AB = a, \(AD = a\sqrt 3 \) và \(\widehat {ASB} = 60^\circ \). Tính diện tích khối cầu ngoại tiếp hình chóp S.ABCD.
A. \(S = \frac{{13\pi {a^2}}}{2}\).
B. \(S = \frac{{13\pi {a^2}}}{3}\).
C. \(S = \frac{{11\pi {a^2}}}{2}\).
D. \(S = \frac{{11\pi {a^2}}}{3}\).
Đáp án đúng là: B
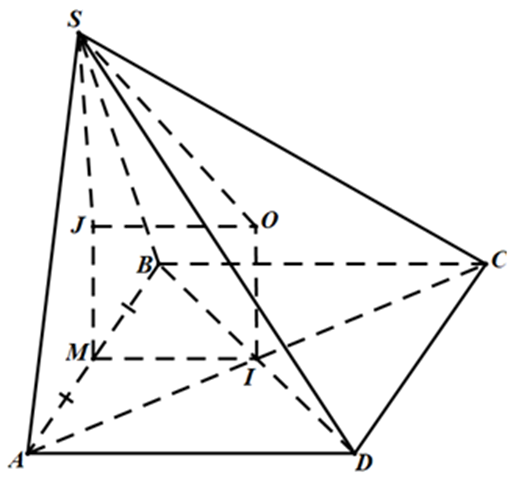
Gọi I, J lần lượt là tâm đường tròn ngoại tiếp hình chữ nhật ABCD và tam giác SAB.
Gọi M là trung điểm của AB và O là tâm của mặt cầu ngoại tiếp hình chóp S.ABCD.
Ta có JM ⊥ AB và IM ⊥ AB.
Mà (SAB) ⊥ (ABCD).
Do đó IM ⊥ JM (1)
Ta có O là tâm của mặt cầu ngoại tiếp hình chóp.
Suy ra OI ⊥ (ABCD).
Do đó OI ⊥ IM (2)
Ta có O là tâm của mặt cầu ngoại tiếp hình chóp.
Suy ra OJ ⊥ (SAB).
Do đó OJ ⊥ JM (3)
Từ (1), (2), (3), suy ra bốn điểm O, J, M, I đồng phẳng và tứ giác OJMI là hình chữ nhật (do có 3 góc ở đỉnh là góc vuông).
Gọi R, Rb lần lượt là bán kính mặt cầu ngoại tiếp khối chóp S.ABCD và bán kính đường tròn ngoại tiếp tam giác SAB.
Áp dụng định lí Pytago, ta được: \(I{A^2} = \frac{{A{C^2}}}{4} = \frac{{B{D^2}}}{4} = \frac{{A{B^2} + A{D^2}}}{4} = \frac{{{a^2} + 3{a^2}}}{4} = {a^2}\).
Áp dụng định lí sin trong tam giác SAB, ta được: \({R_b} = \frac{{AB}}{{2\sin \widehat {ASB}}} = \frac{a}{{2.\sin 60^\circ }} = \frac{{a\sqrt 3 }}{3}\).
Ta có \(R = SO = \sqrt {S{J^2} + O{J^2}} = \sqrt {R_b^2 + I{M^2}} = \sqrt {R_b^2 + I{A^2} - A{M^2}} \).
\( = \sqrt {R_b^2 + I{A^2} - \frac{{A{B^2}}}{4}} = \sqrt {{{\left( {\frac{{a\sqrt 3 }}{3}} \right)}^2} + {a^2} - \frac{{{a^2}}}{4}} = \frac{{a\sqrt {39} }}{6}\).
Vậy diện tích khối cầu ngoại tiếp hình chóp S.ABCD là: \(S = 4\pi {R^2} = \frac{{13\pi {a^2}}}{3}\).
Do đó ta chọn phương án B.