Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N, P lần lượt là trung điểm của các đoạn BC, CD, SO. Tìm giao tuyến của (MNP) với các mặt phẳng (SAB), (SAD), (SBC) và (SCD).
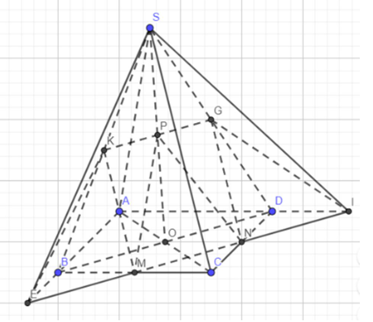
Gọi I, E lần lượt là giao điểm của MN với AD, AB
Qua P kẻ đường thẳng song song với BD cắt SB, SD lần lượt tại K, G
Ta có:
M, N lần lượt là trung điểm của BC, CD ⇒ MN là đường trung bình của ∆BCD ⇒ MN // BD
Mà KG // BD ⇒ MN // KG ⇒ K, G ∈ (MNP)
Ta có:
+) \(\left\{ {\begin{array}{*{20}{c}}{E = AB \cap MN \Rightarrow E \in \left( {SAB} \right) \cap \left( {MNP} \right)}\\{K \in SB;K \in \left( {MNP} \right) \Rightarrow K \in \left( {SAB} \right) \cap \left( {MNP} \right)}\end{array}} \right. \Rightarrow \left( {SAB} \right) \cap \left( {MNP} \right) = KE\)
+) \(\left\{ {\begin{array}{*{20}{c}}{I = AD \cap MN \Rightarrow I \in \left( {SAD} \right) \cap \left( {MNP} \right)}\\{G \in SD;G \in \left( {MNP} \right) \Rightarrow G \in \left( {SAD} \right) \cap \left( {MNP} \right)}\end{array}} \right. \Rightarrow \left( {SAD} \right) \cap \left( {MNP} \right) = IG\)
+) \(\left\{ {\begin{array}{*{20}{c}}{M,K \in \left( {MNP} \right)}\\{M,K \in \left( {SBC} \right)}\end{array}} \right. \Rightarrow \left( {SBC} \right) \cap \left( {MNP} \right) = MK\)
+) \(\left\{ {\begin{array}{*{20}{c}}{N,G \in \left( {MNP} \right)}\\{N,G \in \left( {SCD} \right)}\end{array}} \right. \Rightarrow \left( {SCD} \right) \cap \left( {MNP} \right) = NG\)
Vậy (SAB) ∩ (MNP) = KE; (SAD) ∩ (MNP) = IG; (SBC) ∩ (MNP) = MK; (SCD) ∩ (MNP) = NG.