Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N, P

Đề bài: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N, P lần lượt là trung điểm của các đoạn BC, CD, SO. Tìm giao tuyến của (MNP) với các mặt phẳng (SAB), (SAD), (SBC) và (SCD).

Trả lời

Hướng dẫn giải:

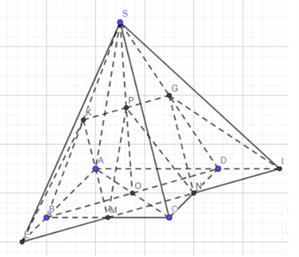
Gọi I, E lần lượt là giao điểm của MN với AD, AB

Qua P  kẻ đường thẳng song song với BD cắt SB, SD lần lượt tại K, G

Ta có:

M, N lần lượt là trung điểm của BC, CD ⇒ MN là đường trung bình của ∆BCD ⇒ MN // BD

Mà KG // BD ⇒ MN // KG ⇒ K, G ∈ (MNP)

Ta có:

+) $\left\{\begin{array}{c}E=AB\cap MN\Rightarrow E\in \left(SAB\right)\cap \left(MNP\right)\\ K\in SB;K\in \left(MNP\right)\Rightarrow K\in \left(SAB\right)\cap \left(MNP\right)\end{array}\right.\Rightarrow \left(SAB\right)\cap \left(MNP\right)=KE$

+) $\left\{\begin{array}{c}I=AD\cap MN\Rightarrow I\in \left(SAD\right)\cap \left(MNP\right)\\ G\in SD;G\in \left(MNP\right)\Rightarrow G\in \left(SAD\right)\cap \left(MNP\right)\end{array}\right.\Rightarrow \left(SAD\right)\cap \left(MNP\right)=IG$

+) $\left\{\begin{array}{c}M,K\in \left(MNP\right)\\ M,K\in \left(SBC\right)\end{array}\right.\Rightarrow \left(SBC\right)\cap \left(MNP\right)=MK$

+) $\left\{\begin{array}{c}N,G\in \left(MNP\right)\\ N,G\in \left(SCD\right)\end{array}\right.\Rightarrow \left(SCD\right)\cap \left(MNP\right)=NG$

Vậy (SAB) ∩ (MNP) = KE; (SAD) ∩ (MNP) = IG; (SBC) ∩ (MNP) = MK; (SCD) ∩ (MNP) = NG.