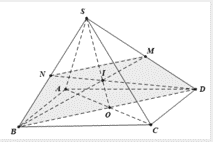
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O

Đề bài: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Lấy điểm I trên đoạn SO sao cho $\frac{SI}{SO}=\frac{2}{3}$, BI cắt SD tại M và DI cắt SB tại N. MNBD là hình gì ?

A. Hình thang. 

B. Hình bình hành. 

C. Hình chữ nhật. 

D. Tứ diện vì MN và BD chéo nhau.

Trả lời

Hướng dẫn giải:

Đáp án đúng là: A

+) Tam giác SBD có SO là đường trung tuyến; điểm I nằm trên đoạn SO; $\frac{SI}{SO}=\frac{2}{3}$.

 nên I là trọng tâm tam giác SBD.

⇒ M là trung điểm SD, N là trung điểm SB.

+) Tam giác SBD có MN là đường trung bình nên MN// BD và $MN=\frac{1}{2}SD$

⇒ Nên MNBD là hình thang.