Cho hình chóp S.ABCD có AC cắt BD tại O. Gọi α, β lần lượt là số đo của các góc nhị diện [A, SO, B] và [B, SO, C]

Bài 30 trang 100 SBT Toán 11 Tập 2: Cho hình chóp S.ABCD có AC cắt BD tại O. Gọi α, β lần lượt là số đo của các góc nhị diện [A, SO, B] và [B, SO, C]. Tính α + β.

Trả lời

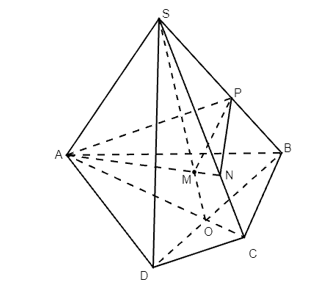
Trong (SAC): Kẻ AN ⊥ SO (N ∈ SC), gọi M = AN ∩ SO (M ∈ SO).

Trong (SOB): Kẻ PM ⊥ SO tại M (P ∈ SB).

· Ta có: AM ⊥ SO, PM ⊥ SO và AM ∩ PM = M ∈ SO.

Suy ra $\widehat{AMP}$ là góc phẳng nhị diện của góc nhị diện [A, SO, B], tức là $\alpha =\widehat{AMP}.$

· Lại có: NM ⊥ SO, PM ⊥ SO và NM ∩ PM = M ∈ SO.

Suy ra $\widehat{PMN}$ là góc phẳng nhị diện của góc nhị diện [B, SO, C], tức là $\beta =\widehat{PMN}.$

Suy ra: $\alpha +\beta =\widehat{AMP}+\widehat{PMN}=\widehat{AMN.}$

Trong (APN) có: M ∈ AN nên 3 điểm A, M, N thẳng hàng, do đó $\widehat{AMN}=180°.$

Từ đó ta có: α + β = 180°.

Xem thêm các bài giải SBT Toán lớp 11 Cánh diều hay, chi tiết khác:

Bài 1: Hai đường thẳng vuông góc

Bài 2: Đường thẳng vuông góc với mặt phẳng

Bài 3: Góc giữa đường thẳng và mặt phẳng. Góc nhị diện

Bài 4: Hai mặt phẳng vuông góc

Bài 5: Khoảng cách

Bài 6: Hình lăng trụ đứng. Hình chóp đều. Thể tích của một số hình khối