Cho hình chóp S.ABCD, ABCD là hình bình hành, M là trung điểm của SA
Đề bài: Cho hình chóp S.ABCD, ABCD là hình bình hành, M là trung điểm của SA.
a) Xác định giao điểm của SB và (MCD).
b) Tìm thiết diện của hình chóp S.ABCD khi cắt bởi (MCD).
Hướng dẫn giải
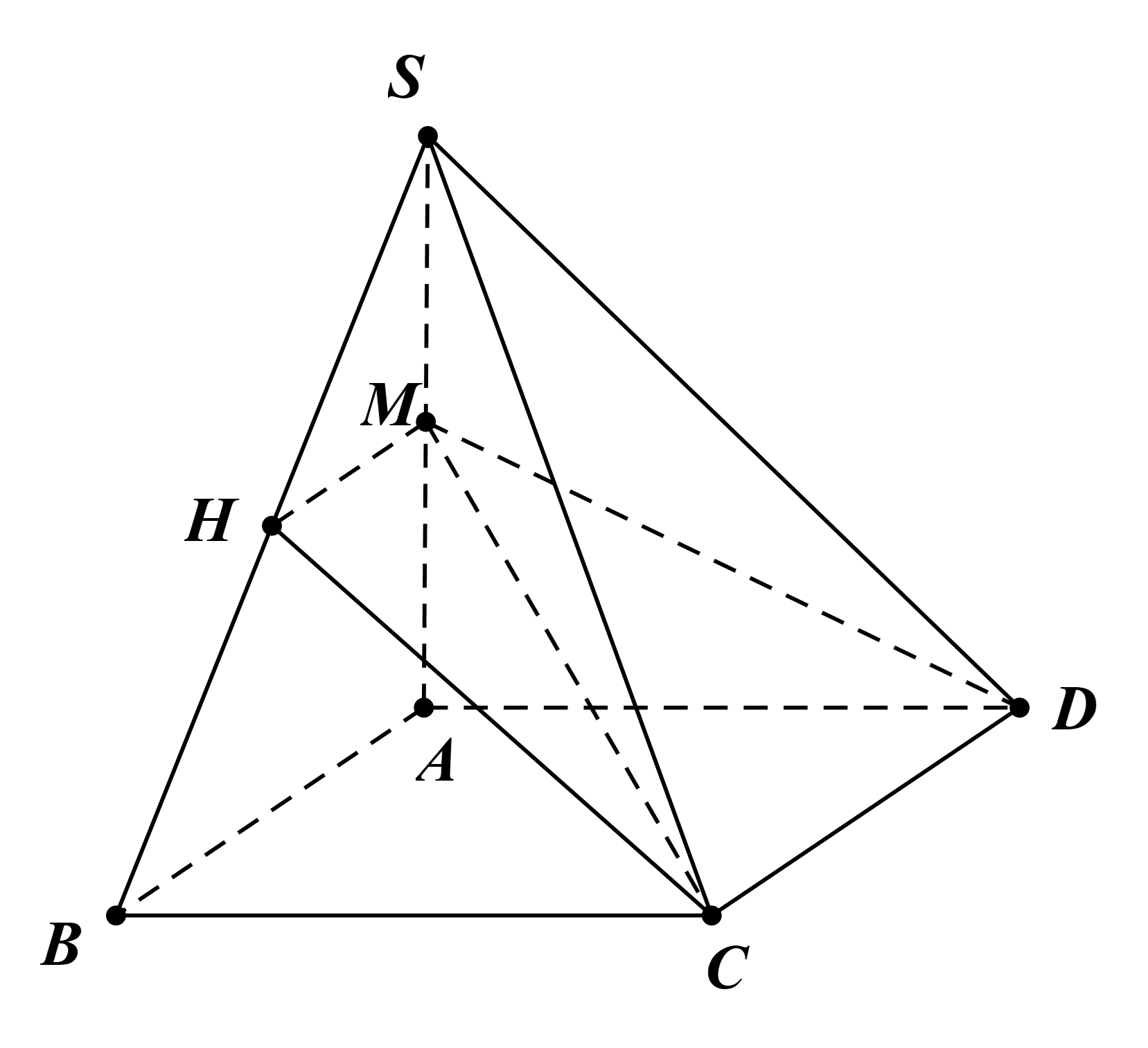
a) Ta có: AB // CD (do ABCD là hình bình hành) và M ∈ (SAB) ∩ (MCD).
Suy ra MH = (SAB) ∩ (MCD), với MH // AB, H ∈ SB.
Vậy giao điểm của SB và (MCD) là H.
b) Ta có:
+ MH = (SAB) ∩ (MCD).
+ HC = (SBC) ∩ (MCD).
+ CD = (SCD) ∩ (MCD).
+ DM = (SAD) ∩ (MCD).
+ MH // CD (do MH // AB, AB //CD).
Vậy thiết diện cần tìm là hình thang MHCD