Cho hình chóp S.ABC có SA vuông góc với (ABC), SA = a và đáy ABC là tam giác vuông tại A

Bài 7.38 trang 41 SBT Toán 11 Tập 2: Cho hình chóp S.ABC có SA $\perp$ (ABC), SA = a và đáy ABC là tam giác vuông tại A, AB = a, AC = a$\sqrt{3}$. Kẻ AM vuông góc với SB tại M, AN vuông góc với SC tại N. Tính theo a thể tích khối chóp S.AMN.

Trả lời

Hướng dẫn. Ta chứng minh được công thức tỉ số khoảng cách sau:

Cho hình chóp S.ABC. Trên các đoạn thẳng SA, SB, SC lần lượt lấy ba điểm A', B', C' khác với S.

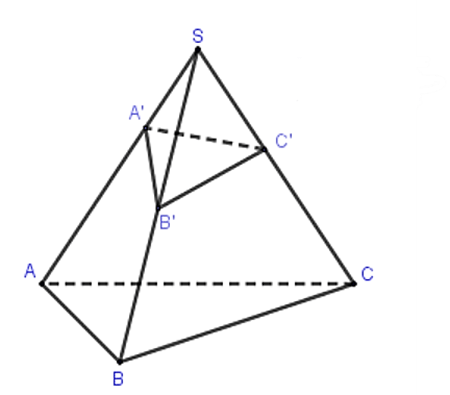
Khi đó ta có: $\frac{V_{S.A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}}}{V_{S.ABC}}=\frac{S{A}^{\text{'}}}{SA}\cdot \frac{S{B}^{\text{'}}}{SB}\cdot \frac{S{C}^{\text{'}}}{SC}$.

Áp dụng công thức trên với bài tập 7.38, ta có $\frac{V_{S.AMN}}{V_{S.ABC}}=\frac{SA}{SA}\cdot \frac{SM}{SB}\cdot \frac{SN}{SC}=\frac{SM}{SB}\cdot \frac{SN}{SC}$.

Trình bày lời giải

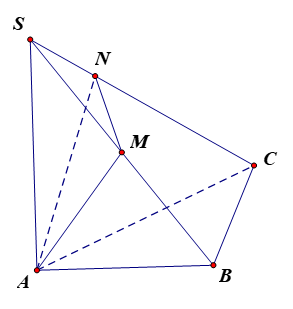
Ta có $V_{S.ABC}=\frac{1}{3}\cdot S_{ABC}\cdot SA$$=\frac{1}{3}\cdot \frac{1}{2}\cdot AB\cdot AC\cdot SA$$=\frac{1}{3}\cdot \frac{1}{2}\cdot a\sqrt{3}\cdot a\cdot a=\frac{a^3\sqrt{3}}{6}$.

Vì SA $\perp$ (ABC) nên SA $\perp$ AB hay tam giác SAB vuông tại A mà SA = AB = a nên tam giác SAB vuông cân tại A.

Vì tam giác SAB vuông cân tại A, AM là đường cao nên AM đồng thời là trung tuyến, suy ra M là trung điểm SB. Do đó $\frac{SM}{SB}=\frac{1}{2}$.

Vì SA $\perp$ (ABC) nên SA $\perp$ AC hay tam giác SAC vuông tại A

Vì tam giác SAC vuông tại A nên $SC=\sqrt{S{A}^2+A{C}^2}=\sqrt{a^2+3a^2}=2a$.

Xét tam giác SAC vuông tại A, đường cao AN có $\frac{SN}{SC}=\frac{SN\cdot SC}{S{C}^2}=\frac{S{A}^2}{S{C}^2}=\frac{1}{4}$.

Do đó $\frac{V_{S.AMN}}{V_{S.ABC}}=\frac{SM}{SB}\cdot \frac{SN}{SC}=\frac{1}{8}$$\Rightarrow V_{S.AMN}=\frac{1}{8}\cdot V_{S.ABC}$$\Rightarrow V_{S.AMN}=\frac{1}{8}\cdot \frac{a^3\sqrt{3}}{6}=\frac{a^3\sqrt{3}}{48}$.

Vậy $V_{S.AMN}=\frac{a^3\sqrt{3}}{48}$ .

Xem thêm các bài giải SBT Toán lớp 11 Kết nối tri thức hay, chi tiết khác: