Lời giải
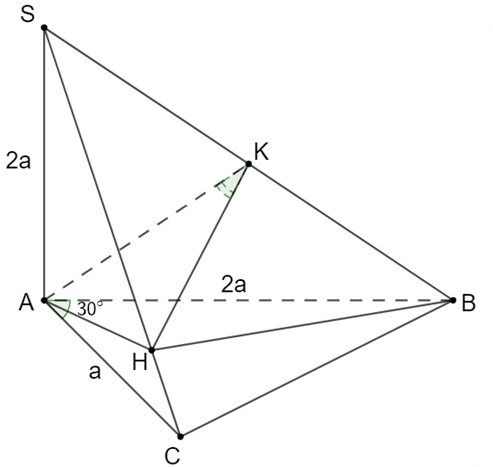
Trong mặt phẳng (SAC), kẻ HI // SA thì HI ^ (ABC).
Ta có: \(CA = AB.\cos 30^\circ = a\sqrt 3 \).
Do đó: \({S_{ABC}} = \frac{1}{2}AB.AC.\sin 30^\circ = \frac{1}{2}.2a.a\sqrt 3 .\sin 30^\circ = \frac{{{a^2}\sqrt 3 }}{2}\).
Ta có: \(\frac{{HI}}{{SA}} = \frac{{HC}}{{SC}} = \frac{{HC.SC}}{{S{C^2}}} = \frac{{A{C^2}}}{{S{C^2}}}\)
\( = \frac{{A{C^2}}}{{S{A^2} + A{C^2}}} = \frac{{3{a^2}}}{{4{a^2} + 3{a^2}}} = \frac{3}{7}\).
\( \Rightarrow HI = \frac{6}{7}a\)
Vậy \({V_{H.ABC}} = \frac{1}{3}{S_{ABC}}.HI = \frac{1}{3}.\frac{{{a^2}\sqrt 3 }}{2}.\frac{6}{7}a = \frac{{{a^3}\sqrt 3 }}{7}\)
Gọi K là hình chiếu vuông góc của A lên SB. Ta có:
AH ^ SC, AH ^ CB (Do CB ^ (SAC)).
Lại có: SB ^ AK Þ SB ^ (AHK).
Do đó, góc giữa hai mặt phẳng (SAB), (SBC) là \(\widehat {HKA}\).
\(\frac{1}{{A{H^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{A{C^2}}} = \frac{1}{{4{a^2}}} + \frac{1}{{3{a^2}}} = \frac{7}{{12{a^2}}} \Rightarrow AH = \frac{{2a\sqrt 3 }}{{\sqrt 7 }}\);
\(\frac{1}{{A{K^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{A{B^2}}} = \frac{1}{{4{a^2}}} + \frac{1}{{4{a^2}}} = \frac{1}{{2{a^2}}} \Rightarrow AK = a\sqrt 2 \).