Cho hình chóp S.ABC có đáy là tam giác $ABC$ vuông tại B có $AB=3,BC=4.$ Biết rằng các mặt bên của khối chóp đều tạo với đáy một góc bằng nhau và bằng $\alpha$ với $\tan \alpha =\frac{5\sqrt{3}}{6},$ đồng thời chân đường cao của hình chóp nằm ở miền trong $△ABC.$Thể tích khối chóp đã cho là

Chọn B

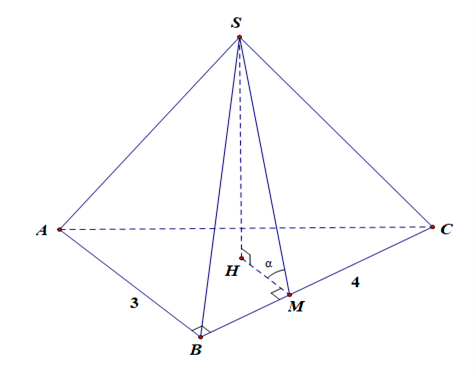
Gọi H là tâm đường tròn nội tiếp của $△ABC.$
Ta có các mặt bên của khối chóp đều tạo với đáy một góc bằng nhau chân đường cao của hình chóp nằm ở miền trong $△ABC.$ nên $SH\perp \left(ABC\right)$

Từ H kẻ $HM\perp BC\left(M\in BC\right)$
Suy ra $HM\text{//}AB;SM\perp BC$$\Rightarrow \widehat{SMH}=\alpha .$
$S_{ABC}=\frac{1}{2}AB.BC=6;BC=5.$
Ta có $HM=r=\frac{S_{ABC}}{\frac{AB+BC+AC}{2}}=\frac{6}{6}=1$
Xét $△SHM$: $SH=HM.\tan \alpha =\frac{5\sqrt{3}}{6}$
Vậy $V_{S.ABC}=\frac{1}{3}{S}_{ABC}.SH=\frac{1}{3}\mathrm{.6.}\frac{5\sqrt{3}}{6}=\frac{5\sqrt{3}}{3}$