Lời giải
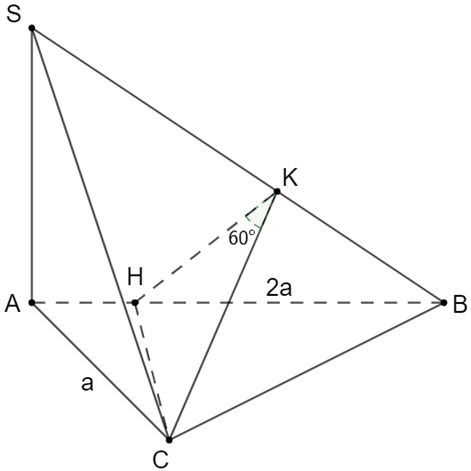
Trong ∆ABC kẻ CH ^ AB
Mà SA ^ CH (SA ^ (SAB))
Þ CH ^ (SAB) Þ CH ^ SB (1)
\(BC = \sqrt {A{B^2} - A{C^2}} = a\sqrt 3 \)
\(BH.BA = B{C^2} \Rightarrow BH = \frac{{3a}}{2}\)
\(CH = \sqrt {B{C^2} - B{H^2}} = \frac{{\sqrt 3 }}{2}a\)
Trong ∆SAB kẻ HK ^ SB (2)
Từ (1) và (2) Þ SB ^ (HKC)
Þ SB ^ KC
Góc giữa hai mặt phẳng (SAB) và (SBC) là \(\widehat {CKH} = 60^\circ \)
Trong tam giác vuông CKH có:
\(HK = CH.\cot 60^\circ = \frac{1}{2}a\)
\(BK = \sqrt {B{H^2} - H{K^2}} = a\sqrt 2 \)
Xét ∆SAB và ∆HKB có:
\(\widehat {SAB} = \widehat {HKB} = 90^\circ \)
\(\widehat B\): góc chung
Þ ∆SAB ᔕ ∆HKB (g.g)
\( \Rightarrow \frac{{SA}}{{HK}} = \frac{{AB}}{{BK}} = \frac{{2a}}{{a\sqrt 2 }} \Rightarrow SA = \frac{a}{{\sqrt 2 }}\).
Thể tích của khối chóp S.ABC là:
\(V = \frac{1}{3}SA.{S_{ABC}} = \frac{1}{3} \cdot \frac{a}{{\sqrt 2 }} \cdot \frac{1}{2} \cdot a\sqrt 3 \cdot a = \frac{{{a^3}\sqrt 6 }}{{12}}\).
Tam giác HKA vuông tại H (vì AH ^ (SBC), HK Ì (SBC))
\(\sin \widehat {HKA} = \frac{{AH}}{{AK}} = \frac{{\frac{{2a\sqrt 3 }}{{\sqrt 7 }}}}{{a\sqrt 2 }} = \frac{{\sqrt 6 }}{{\sqrt 7 }} \Rightarrow \cos \widehat {HKA} = \frac{{\sqrt 7 }}{7}\).