Cho hình chóp S.ABC có A’, B’, C’ lần lượt là trung điểm của SA, SB, SC. Tìm các đường thẳng lần lượt nằm trong, cắt, song song với mặt phẳng (ABC)
621
16/06/2023
Thực hành 2 trang 109 Toán 11 Tập 1: Cho hình chóp S.ABC có A’, B’, C’ lần lượt là trung điểm của SA, SB, SC. Tìm các đường thẳng lần lượt nằm trong, cắt, song song với mặt phẳng (ABC).
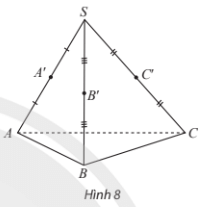
Trả lời
+) Ta có: đường thẳng AB chứa hai điểm A, B thuộc (ABC), suy ra AB ⊂ (ABC).
Tương tự ta có BC ⊂ (ABC), AC ⊂ (ABC)
Vì vậy các đường thẳng nằm trong mặt phẳng (ABC) là: AB, BC, AC.
+) Ta có: đường thẳng SA có điểm A chung với (ABC), duy ra SA cắt (ABC) tại A.
Tương tự ta có: SB, SC lần lượt cắt (ABC) tại B, C.
Vì vậy các đường thẳng cắt mặt phẳng (ABC) là: SA, SB, SC.
+) Ta có: A’B’ // AB mà AB ⊂ (ABC) nên A’B’ // (ABC).
Tương tự ta có: A’C’ // (ABC) và B’C’ // (ABC).
Xem thêm các bài giải SGK Toán 11 Chân trời sáng tạo hay, chi tiết khác:
Bài 1: Điểm, đường thẳng và mặt phẳng trong không gian
Bài 2: Hai đường thẳng song song
Bài 3: Đường thẳng và mặt phẳng song song
Bài 4: Hai mặt phẳng song song
Bài 5: Phép chiếu song song
Bài tập cuối chương 4

