Bài 4 trang 112 Toán 11 Tập 1: Cho tứ diện ABCD và điểm M thuộc cạnh AB. Gọi (α) là mặt phẳng qua M, song song với hai đường thẳng BC và AD. Gọi N, P, Q lần lượt là giao điểm của mặt phẳng (α) với các cạnh AC, CD và DB.
a) Chứng minh MNPQ là hình bình hành.
b) Trong trường hợp nào thì MNPQ là hình thoi?
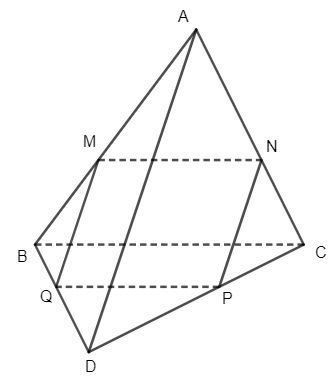
a) Trong mặt phẳng (ABC) từ điểm M kẻ đường thẳng song song với BC cắt AC tại N.
Trong mặt phẳng (ACD) từ điểm N kẻ đường thẳng song song với AD cắt cạnh CD tại P.
Trong mặt phẳng (BCD) từ điểm P kẻ đường thẳng song song với BC cắt cạnh BD tại Q.
Nối M với Q lại ta được mặt phẳng (MNPQ) chính là mặt phẳng (α) cần dựng.
Xét tứ giác MNPQ, có:
MN // QP (cùng // BC)
MQ // NP (cùng //AD)
Do đó tứ giác MNPQ là hình bình hành (theo dấu hiệu nhận biết).
b) Để tứ giác MNPQ là hình thoi thì MN = NP, điều này xảy ra trong trường hợp M là trung điểm của AB và AD = BC.
Xem thêm các bài giải SGK Toán 11 Chân trời sáng tạo hay, chi tiết khác:
Bài 1: Điểm, đường thẳng và mặt phẳng trong không gian
Bài 2: Hai đường thẳng song song
Bài 3: Đường thẳng và mặt phẳng song song