Cho hình bình hành có AB = 2AD. Gọi M, N theo thứ tự là trung điểm

Đề bài: Cho hình bình hành có AB = 2AD. Gọi M, N theo thứ tự là trung điểm của AB và CD.

a) Chứng minh tứ giác AMCN là hình bình hành.

b) Chứng minh AN vuông góc với DM.

c) Gọi E là giao điểm của AN và DM, F là giao điểm của MC và BN. Chứng minh EF = MN.

d) Chứng minh diện tích hình bình hành ABCD gấp 4 lần diện tích tam giác ADN.

Trả lời

Hướng dẫn giải:

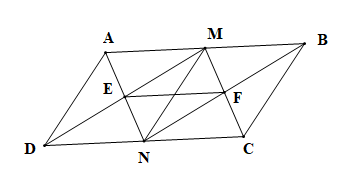
a) Vì ABCD là hình bình hành

Nên AB = CD, AB // CD

Vì M, N theo thứ tự là trung điểm của AB và CD

Nên AM = MB = $\frac{1}{2}$ AB, CN = DN = $\frac{1}{2}$ CD

Mà AB = CD (chứng minh trên)

Suy ra AM = CN = MB = DN

Xét tứ giác AMCN có

AM = CN, AM // CN (chứng minh trên)

Suy ra AMCN là hình bình hành

Vậy AMCN là hình bình hành.

b) Xét tứ giác AMND có

AM = DN, AM // DN (chứng minh trên)

Suy ra AMND là hình bình hành

Ta có AB = 2AM, AB = 2AD

Suy ra AM = AD

Mà AMND là hình bình hành

Do đó AMND là hình thoi

Lại có AN, DM là hai đường chéo

Suy ra AN ⊥ DM

Vậy AN ⊥ DM.

c) Xét tứ giác BMNC có

BM = CN, BM // CN (chứng minh câu a)

Suy ra BMNC là hình bình hành

Mà hai đường chéo MC và BN cắt nhau tại F

Suy ra F là trung điểm của MC, BN

Do đó MF = $\frac{1}{2}$ MC

Vì AMND là hình bình hành có hai đường chéo AN, DM cắt nhau tại E

Nên E là trung điểm của AN

Suy ra NE = $\frac{1}{2}$ AN

Vì AMCN là hình bình hành nên AN // CM, AN = CM

Ta có MF = $\frac{1}{2}$ MC, NE = $\frac{1}{2}$ AN, AN = CM

Suy ra MF = NE

Xét tứ giác EMFN có

FM = EN, FM // EN (chứng minh trên)

Suy ra EMFN là hình bình hành

Mà $\widehat{MEN}=90°$  (do AN ⊥ DM)

Do đó EMFN là hình chữ nhật

Lại có MN và EF là hai đường chéo

Suy ra MN = FE

Vậy MN = FE.

d) Gọi h là chiều cao của hình bình hành ABCD kẻ từ A

Ta có $\frac{S_{ABC\text{D}}}{S_{A\text{D}N}}=\frac{h.C\text{D}}{\frac{1}{2}h.DN}=\frac{2C\text{D}}{DN}=\frac{2.2\text{D}N}{DN}=4$

Suy ra S_ABCD = 4 S_ADN