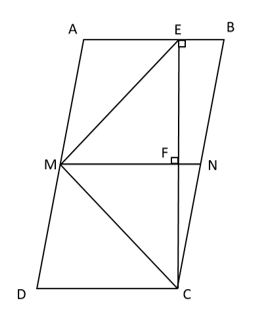
Cho hình bình hành ABCD trong đó có AD = 2AB. Kẻ CE vuông góc với AB. Gọi M là trung điểm của AD, nối EM, kẻ MF vuông góc với CE; MF cắt BC tại N.
27
01/06/2024
Cho hình bình hành ABCD trong đó có AD = 2AB. Kẻ CE vuông góc với AB. Gọi M là trung điểm của AD, nối EM, kẻ MF vuông góc với CE; MF cắt BC tại N.
a) Tứ giác MNCD là hình gì?
Trả lời
a)
Theo đề ta có: CE vuông góc với AB và CE vuông góc với MN.
Suy ra AB // MN.
Mà ABCD là hình bình hành nên AB // CD.
Do đó MN // DC.
Mặc khác M là trung điểm của AD nên AD = 2MN;
Theo đề AD = 2AB = 2DC (vì ABCD là hình hình hành nên AB = DC).
Do đó MN = DC.
Xét tứ giác MNCD có:
MN // DC (cmt)
MN = DC
Suy ra MNCD là hình bình hành.