Cho hình bình hành ABCD, hai đường chéo AC cắt BD tại O, hai đường cao AM và DQ của ∆AOD cắt nhau tại E, 2 đường cao BN và CP của ∆BOC cắt nhau tại F. Chứng minh AMCP, MNPQ là hình bình hành.

Trả lời

Lời giải:

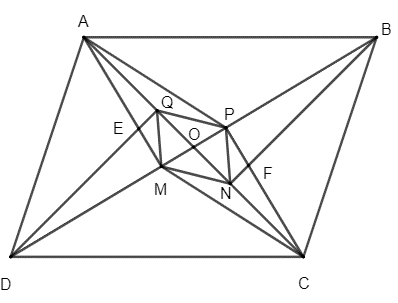
Vì O là giao hai đường chéo của hình bình hành ABCD nên O là trung điểm của AC và BD.

Xét ΔAMO vuông tại M và ΔCPO vuông tại P có

OA = OC (O là trung điểm AC); \(\widehat {AOM} = \widehat {COP}\) (đối đỉnh)

Do đó: ΔAMO = ΔCPO (cạnh huyền – góc nhọn)

⇒ OM = OP hay O là trung điểm của PM.

Xét ΔDQO vuông tại Q và ΔBNO vuông tại N có 

OD = OB (O là trung điểm của BD); \(\widehat {DOQ} = \widehat {BON}\) (đối đỉnh)

Do đó: ΔDQO = ΔBNO (cạnh huyền – góc nhọn)

⇒ OQ = ON hay O là trung điểm của QN

Xét tứ giác AMCP có:

O là trung điểm của AC; O là trung điểm của MP

Do đó: AMCP là hình bình hành.

Xét tứ giác MNPQ có

O là trung điểm của MP; O là trung điểm của NQ.

Do đó: MNPQ là hình bình hành.