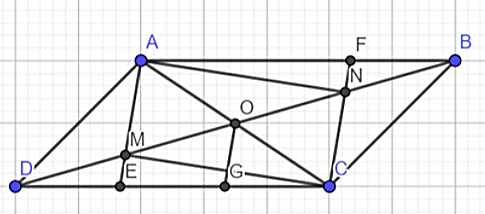
Câu 7: Cho hình bình hành ABCD. Gọi O là giao điểm của 2 đường chéo M, N là trung điểm của OD và OB. Gọi E là giao điểm của AM và CD. F là giao điểm của CN và AB.
a, Chứng minh: Tứ giác AMCN là hình bình hành
b, Tứ giác AECF là hình gì?
c, Chứng minh: E, F đối xứng qua O
d, Chứng minh: EC = 2DE.
Ta có ABCD là hình bình hành ⇒ AC ∩ BD tại trung điểm mỗi đường
Mà AC ∩ BD = 0 ⇒ O là trung điểm AC, DB
Lại có M, N là trung điểm OD, OB
=> OM = 1/2 OD = 1/2 OB = ON
⇒ O là trung điểm MN
Do O là trung điểm AC, MN
⇒ AMCN là hình bình hành (đpcm).
b,
Ta có AMCN là hình bình hành.
⇒ AM // CN
⇒ AE // CF
Mà AB // CD ⇒ AF // CE
⇒ AECF là hình bình hành.
c,
Ta có AECF là hình bình hành.
⇒ AC ∩ EF tại trung điểm mỗi đường
Mà O là trung điểm AC
⇒ O là trung điểm EF
⇒ E, F đối xứng nhau qua O (đpcm).
d,
Gọi G là trung điểm CE
Vì O là trung điểm AC ⇒ OG là đường trung bình ∆ACE
⇒ OG // AE
⇒ ME // OG
Mà M là trung điểm DO ⇒ ME là đường trung bình ∆ODG
⇒ E là trung điểm DG
⇒ DE = EG = GC
⇒ CE = CG + GE = DE + DE = 2DE (đpcm).