Cho hình bình hành ABCD. Gọi M là điểm nằm giữa A và B, N là điểm nằm giữa C và D sao cho AM = CN

Bài 11 trang 121 Toán 8 Tập 1: Cho hình bình hành ABCD. Gọi M là điểm nằm giữa A và B, N là điểm nằm giữa C và D sao cho AM = CN. Gọi I là giao điểm của MN và AC. Chứng minh:

a) ΔIAM = ΔICN;

b) Tứ giác AMCN là hình bình hành;

c) Ba điểm B, I, D thẳng hàng.

Trả lời

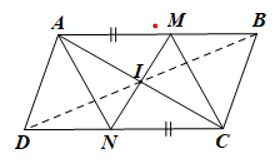
a) Do ABCD là hình bình hành nên AB // CD.

Suy ra $\widehat{AMN}=\widehat{CNM}$ và $\widehat{MAC}=\widehat{NCM}$ (các cặp góc so le trong)

Xét ΔIAM và ΔICN có:

$\widehat{AMI}=\widehat{CNI}$ (do $\widehat{AMN}=\widehat{CNM}$);

AM = CN (giả thiết);

$\widehat{MAI}=\widehat{NCI}$ (do $\widehat{MAC}=\widehat{NCM}$)

Do đó ΔIAM = ΔICN (g.c.g)

b) Xét tứ giác AMCN có AM = CN (giả thiết) và AM // CN (do AB // CD)

Suy ra tứ giác AMCN là hình bình hành.

c) Do AMCN là hình bình hành nên hai đường chéo AC, MN cắt nhau tại trung điểm I của mỗi đường.

Do ABCD là hình bình hành nên hai đường chéo AC, BD cắt nhau tại trung điểm của mỗi đường.

Mà I là trung điểm của AC nên I là trung điểm của BD.

Do đó ba điểm B, I, D thẳng hàng.

Xem thêm các bài giải SGK Toán lớp 8 Cánh Diều hay, chi tiết khác:

Bài 3: Hình thang cân

Bài 4: Hình bình hành