Cho hình vuông ABCD. Trên các cạnh AB, BC, CD, DA lần lượt lấy các điểm M, N, P, Q sao cho AM = BN = CP = DQ < AB

Bài 10 trang 121 Toán 8 Tập 1:Cho hình vuông ABCD. Trên các cạnh AB, BC, CD, DA lần lượt lấy các điểm M, N, P, Q sao cho AM = BN = CP = DQ < AB. Chứng minh tứ giác MNPQ là hình vuông.

Trả lời

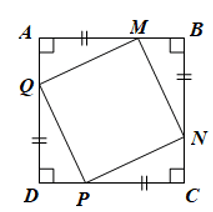
• Do ABCD là hình vuông nên AB = BC = CD = DA.

Mà AM = BN = CP = DQ

Suy ra AB – AM = BC – BN = CD – CP = DA – DQ

Hay MB = NC = PD = QA

• Xét ΔAMQ và ΔBNM có:

$\widehat{MAQ}=\widehat{NBM}=90°$;

AM = BN (giả thiết);

QA = MB (chứng minh trên)

Do đó ΔAMQ = ΔBNM (hai cạnh góc vuông)

Suy ra QM = MN (hai cạnh tương ứng).

Chứng minh tương tự ta có: MN = NP và NP = PQ.

Khi đó MN = NP = PQ = QM.

• Tứ giác MNPQ có 4 cạnh bằng nhau nên là hình thoi.

• Do ΔAMQ = ΔBNM (chứng minh trên) nên $\widehat{AMQ}=\widehat{BNM}$ (hai góc tương ứng)

Mà $\widehat{BNM}+\widehat{BMN}=90°$ (do ΔBMN vuông tại B)

Suy ra $\widehat{AMQ}+\widehat{BMN}=90°$

Lại có $\widehat{AMQ}+\widehat{QMN}+\widehat{BMN}=180°$

Suy ra $\widehat{QMN}=180°-\left(\widehat{AMQ}+\widehat{BMN}\right)=180°-90°=90°$.

• Hình thoi MNPQ có $\widehat{QMN}=90°$ nên là hình vuông.

Xem thêm các bài giải SGK Toán lớp 8 Cánh Diều hay, chi tiết khác:

Bài 3: Hình thang cân

Bài 4: Hình bình hành