Cho hình bình hành ABCD. Gọi d là đường thẳng qua A và không cắt đoạn thẳng BD

Đề bài: Cho hình bình hành ABCD. Gọi d là đường thẳng qua A và không cắt đoạn thẳng BD. Gọi BB’, CC’, DD’ lần lượt là khoảng cách từ B, C, D đến đường thẳng d (B’, C’, D’ ∈ (d)). Chứng minh rằng BB’ + DD’ = CC’.

Trả lời

Hướng dẫn giải:

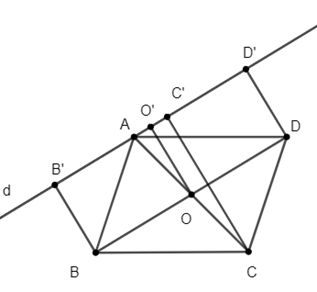
Gọi O là giao điểm của AC và BD. ABCD là hình bình hành nên O là trung điểm của AC và BD. Vẽ OO’⊥ d, O’ ∈ d.

Các đường thẳng BB’, CC’, DD’, OO’ song song với nhau (vì cùng vuông góc với đường thẳng d).

Vì B’D’DB là hình thang (vì BB’ // DD) có OB = OD, OO’ // BB’ nên OO’ là đường trung bình của hình thang  B’D’DB.

Do đó $OO\text{'}=\frac{1}{2}\left(BB\text{'}+DD\text{'}\right)$.

Mặt khác ∆ACC’ có OO’ // CC’ và OA = OC.

Nên OO’ là đường trung bình của tam giác ACC’, suy ra: $OO\text{'}=\frac{1}{2}CC\text{'}$.

Từ (1) và (2) suy ra BB’ + DD’ = CC’.