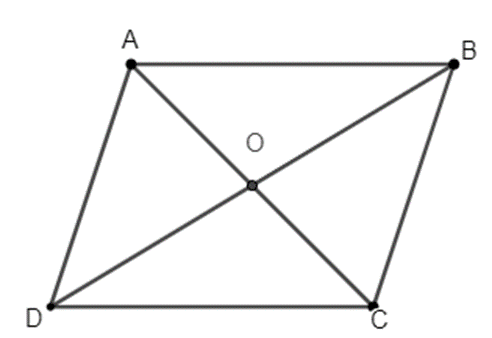
Cho hình bình hành ABCD có tâm O. Tìm vecto từ 5 điểm A, B, C, D bằng \(\overrightarrow {AB} ;\,\,\overrightarrow {OB} \).

A. \(\overrightarrow {AB} = \overrightarrow {AC} ,\overrightarrow {OB} = \overrightarrow {AO} \);

B. \(\overrightarrow {AB} = \overrightarrow {OC} ;\overrightarrow {OB} = \overrightarrow {DO} \);

C. \(\overrightarrow {AB} = \overrightarrow {DC} ;\overrightarrow {OB} = \overrightarrow {AO} \);

D. \(\overrightarrow {AB} = \overrightarrow {DC} ;\overrightarrow {OB} = \overrightarrow {DO} \).

Đáp án đúng là: D.

Vì ABCD là hình bình hành ta có: AB = DC; OB = OD.

Mà ta có hai vectơ bằng nhau nếu chúng cùng hướng và độ dài nên: \(\overrightarrow {AB} = \overrightarrow {DC} ;\,\,\overrightarrow {OB} = \overrightarrow {DO} \).