Cho hình bình hành ABCD có AB > BC. Đường phân giác của góc D cắt AB tại M, đường phân giác của góc B cắt CD tại N.
a) Chứng minh: AM = CN.
b) Chứng minh: tứ giác DMBN là hình bình hành.
Lời giải
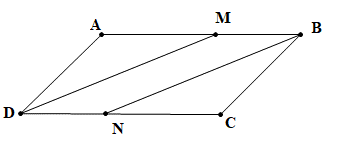
a) Vì ABCD là hình bình hành nên AB // CD
Suy ra \(\widehat {AM{\rm{D}}} = \widehat {M{\rm{D}}C}\) (Hai góc so le trong) và AB = CD, AD = BC (1)
Vì DM là tia phân giác của góc ADC ⇒ \(\widehat {ADM} = \widehat {MDC} = \frac{1}{2}\widehat {CDA}\)
Suy ra \(\widehat {AM{\rm{D}}} = \widehat {M{\rm{DA}}}\)
Do đó tam giác ADM cân tại A
Suy ra AM = AD (tính chất) (2)
Vì BN là tia phân giác của góc ABC ⇒ \(\widehat {ABN} = \widehat {NBC} = \frac{1}{2}\widehat {ABC}\)
Vì ABCD là hình bình hành nên AB // CD nên \(\widehat {ABN} = \widehat {BNC}\) (Hai góc so le trong)
Suy ra \(\widehat {CBN} = \widehat {BNC}\)
Do đó tam giác BCN cân tại C
Suy ra CN = CB (tính chất) (3)
Từ (1), (2) và (3) suy ra AM = CN
Vậy AM = CN
b) Ta có:
AB = AM + MB
CD = CN + ND
Mà AB = CD, AM = CN (chứng minh câu a)
Suy ra MB = ND
Tứ giác DMBN có:
MB = ND (chứng minh trên)
MB // ND (vì AB // CD)
Suy ra DMBN là hình bình hành
Vậy DMBN là hình bình hành.