Cho hình bình hành ABCD có AB = 2AD. Gọi E, F thứ tự là trung điểm của AB và CD

Đề bài: Cho hình bình hành ABCD có AB = 2AD. Gọi E, F thứ tự là trung điểm của AB và CD

a) Các tứ giác AEFD, AECF là hình gì? Vì sao?

b) Gọi M là giao điểm của AF và DE, gọi N là giao điểm của BF và CE. Chứng minh rằng tứ giác EMFN là hình chữ nhật.

Trả lời

Hướng dẫn giải:

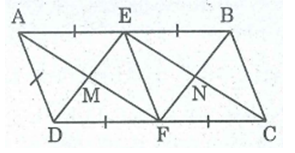
a) Ta có: $AE=DE=\frac{1}{2}AB$  và AE // DF

→ tứ giác AEFD là hình bình hành

Có thêm $AE=AD=\frac{1}{2}AB$

→AEFD là hình thoi (dấu hiệu nhận biết hình thoi)

AE // FC và AE = FC ( vì cùng $=\frac{1}{2}AB$ )

→ AECF là hình bình hành

b) Tứ giác AECF là hình bình hành nên EN // MF(1)

Chứng minh tương tự câu a tứ giác EBFN là hình bình hành

→ ME // FN(2)

Từ (1) và (2) suy ra EMFN là hình bình hành (3)

Tứ giác AEFD là hình thoi nên suy ra $\text{AF}\perp DE$

$\to \widehat{\text{EMF}}={90}^{\circ }$ (4)

Từ (3) và (4) suy ra EMFN là hình chữ nhật