Cho Hình 3.35. Biết CN là tia phân giác của góc ACM. a) Chứng minh rằng CN // AB
Bài 3.35 trang 49 Tập 1: Cho Hình 3.35. Biết CN là tia phân giác của góc ACM.
a) Chứng minh rằng CN // AB.
b) Tính số đo của góc A.
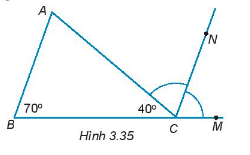
Bài 3.35 trang 49 Tập 1: Cho Hình 3.35. Biết CN là tia phân giác của góc ACM.
a) Chứng minh rằng CN // AB.
b) Tính số đo của góc A.

a) Ta có: ^ACB và ^ACM là hai góc kề bù nên ^ACB + ^ACM = 180o.
Thay số, 40o + ^ACM = 180o
^ACM = 180o – 40o
^ACM = 140o
Vì CN là tia pân giác của góc ^ACM nên ^ACN=^NCM=^ACM2=140°
Ta có: và ở vị trí đồng vị và = = 70o.
Do đó, AB song song CN.
b) Vì AB song song với CN nên các cặp góc so le trong sẽ bằng nhau và các cặp góc đồng vị sẽ bằng nhau.
Ta có: và là hai góc so le trong. Do đó, = = 70o.
Vậy = 70o.
Xem thêm các bài giải SBT Toán lớp 7 Kết nối tri thức hay, chi tiết khác:
Bài 10: Tiên đề Euclid. Tính chất của hai đường thẳng song song
Bài 11: Định lí và chứng minh định lí
Bài 12: Tổng các góc trong một tam giác
Bài 13: Hai tam giác bằng nhau. Trường hợp bằng nhau thứ nhất của tam giác