Cho hàm số f(x) có đạo hàm f'(x). Hàm số y=f'(x) liên tục trên tập số thực và có bảng biến thiên như
Cho hàm số có đạo hàm . Hàm số liên tục trên tập số thực và có bảng biến thiên như sau:
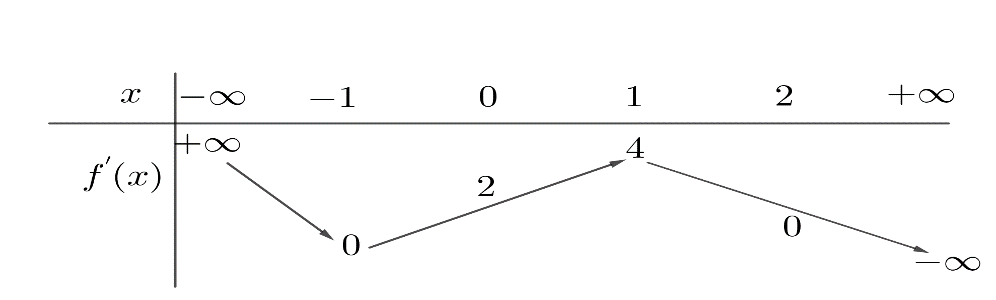
Biết rằng , . Tính giá trị nhỏ nhất của hàm số trên đoạn .
Biết rằng , . Tính giá trị nhỏ nhất của hàm số trên đoạn .
