Cho hàm số: y = m/3 x^3 - (m - 1)x^2 + 3(m - 2)x + 1 để hàm số đạt cực đại x1, x2

Đề bài: Cho hàm số: $y=\frac{m}{3}{x}^3-(m-1)x^2+3(m-2)x+1$ để hàm số đạt cực đại x₁, x₂ thỏa mãn x₁ + 2x₂ = 1 thì giá trị của m bằng?

Trả lời

Hướng dẫn giải:

Ta có: y' = mx² – 2(m – 1)x + 3(m – 2) (m ≠ 0)

Để hàm số có cực đại tại x₁ và cực tiểu tại x₂ thì phương trình

y' = mx2 – 2(m – 1)x + 3(m – 2)  = 0 có 2 nghiệm phân biệt.

 = (m – 1)² – 3m(m – 2) = −2m² + 4m + 1 > 0

$\Rightarrow 1-\frac{\sqrt{6}}{2}<m<1+\frac{\sqrt{6}}{2}$ (1)

Khi đó áp dụng định lý Vi−ét, ta có:

$\left\{\begin{array}{l}{x}_1+x_2=\frac{2(m-1)}{m}\left(2\right)\\ x_1{x}_2=\frac{3(m-2)}{m}\left(3\right)\end{array}\right.$

Mặt khác theo bài cho ta có: x₁ + 2x₂ = 1 (4)

Nếu 2x₁ + x₂ = 0 (5)

Từ (4) và (5) $\Rightarrow x_1=-\frac{1}{3};x_2=\frac{2}{3}$ .

Thay vào (2) ta có: $2\frac{m-1}{m}=\frac{1}{3}\Rightarrow m=\frac{6}{5}$

Thay vào (3) ta có: $3\frac{m-2}{m}=-\frac{2}{9}\Rightarrow m=\frac{54}{9}$

Suy ra 2x₁ + x₂ ≠ 0

Khi đó nhân hai vế của (4) với 2x₁ + x₂ ta có:

(x₁ + 2x₂)(2x₁ + x₂) = 2x₁ + x₂

 2(x₁ + x₂)² + x₁x₂ = 2x₁ + x₂

Thay (2) và (3) vào ta được:

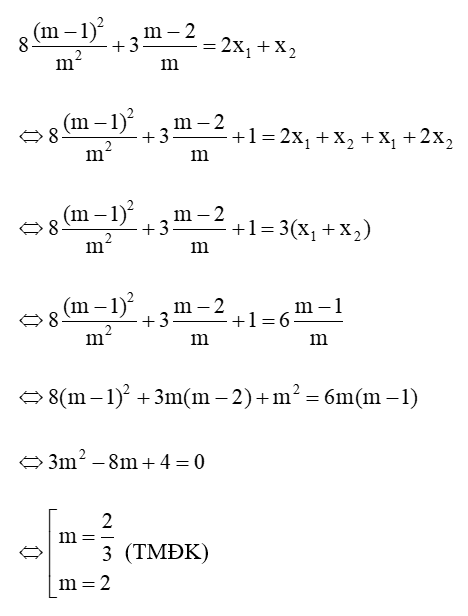
Vậy có hai giá trị m thỏa mãn yêu cầu bài toán là: $m=\frac{2}{3}$ ; m = 2.