Đáp án đúng là: A.

$g\left(x\right)=f\left(x^2-1\right)\Rightarrow g^{\text{'}}\left(x\right)=2x\cdot f^{\text{'}}\left(x^2-1\right)=2x\left(x^2-1\right)x^2\left[{\left(x^2-1\right)}^2-2m\left(x^2-1\right)+1\right]$

Ta có $\iff \left[\begin{array}{l}x=0\\ x^2-1=0\\ x^2=0\\ {\left(x^2-1\right)}^2-2m\left(x^2-1\right)+1=0\end{array}\right.$$\iff \left[\begin{array}{l}x=0\\ x=\pm 1\\ {\left(x^2-1\right)}^2-2m\left(x^2-1\right)+1=0\end{array}\right.$ .

Để hàm số $g\left(x\right)=f\left(x^2-1\right)$  có 7 điểm cực trị thì phương trình ${\left(x^2-1\right)}^2-2m\left(x^2-1\right)+1=0$  phải có 4 đơn nghiệm phân biệt khác x = 0 , $x=\pm 1$ .

Xét phương trình ${\left(x^2-1\right)}^2-2m\left(x^2-1\right)+1=0$

Đặt $t=x^2-1$ , khi đó ta được phương trình $t^2-2mt+1=0$  với $t\ge -1$ .

Với $t>-1$  ta có hai nghiệm x ,

Với t = -1  ta có nghiệm x = 0 ,

Với t < -1  phương trình vô nghiệm.

Nên để ${\left(x^2-1\right)}^2-2m\left(x^2-1\right)+1=0$  có 4 đơn nghiệm phân biệt khi và chỉ khi phương trình $t^2-2mt+1=0$  có hai nghiệm phân biệt $0\ne t>-1$ .

Ta có $t^2-2mt+1=0\iff 2m=t+\frac{1}{t}$ .

Xét hàm số $h\left(t\right)=t+\frac{1}{t}$ , ta có $h^{\text{'}}\left(t\right)=1-\frac{1}{t^2}=0\iff t=\pm 1$ .

Bảng biến thiên:

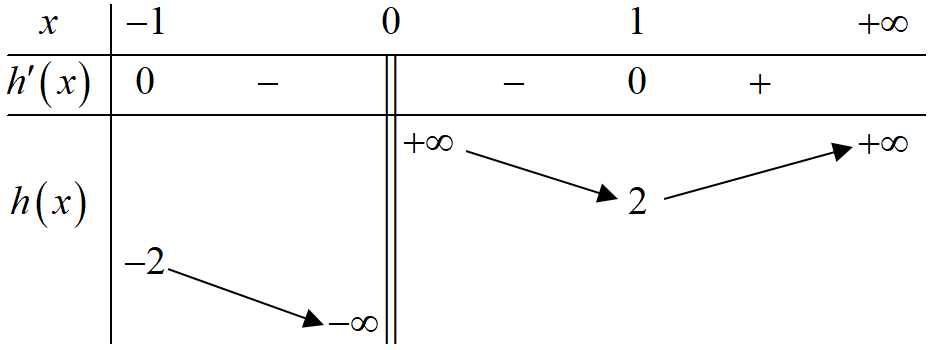
Từ bảng biến thiên, phương trình $t^2-2mt+1=0$  có hai nghiệm phân biệt $0\ne t>-1$   khi m > 2 .