Cho hàm số y = (2 – m)x + m + 1 (với m là tham số và m ≠ 2) có đồ thị là đường thẳng d. a) Khi m = 0, hãy vẽ d trên trục tọa độ Oxy. b) Tìm m để d cắt đường thẳng y = 2x – 5 tại điểm có hoà
25
18/05/2024
Cho hàm số y = (2 – m)x + m + 1 (với m là tham số và m ≠ 2) có đồ thị là đường thẳng d.
a) Khi m = 0, hãy vẽ d trên trục tọa độ Oxy.
b) Tìm m để d cắt đường thẳng y = 2x – 5 tại điểm có hoành độ bằng 2.
c) Tìm m để d cùng với các trục tọa độ Ox, Oy tạo thành một tam giác có diện tích bẳng 2.
Trả lời
Lời giải
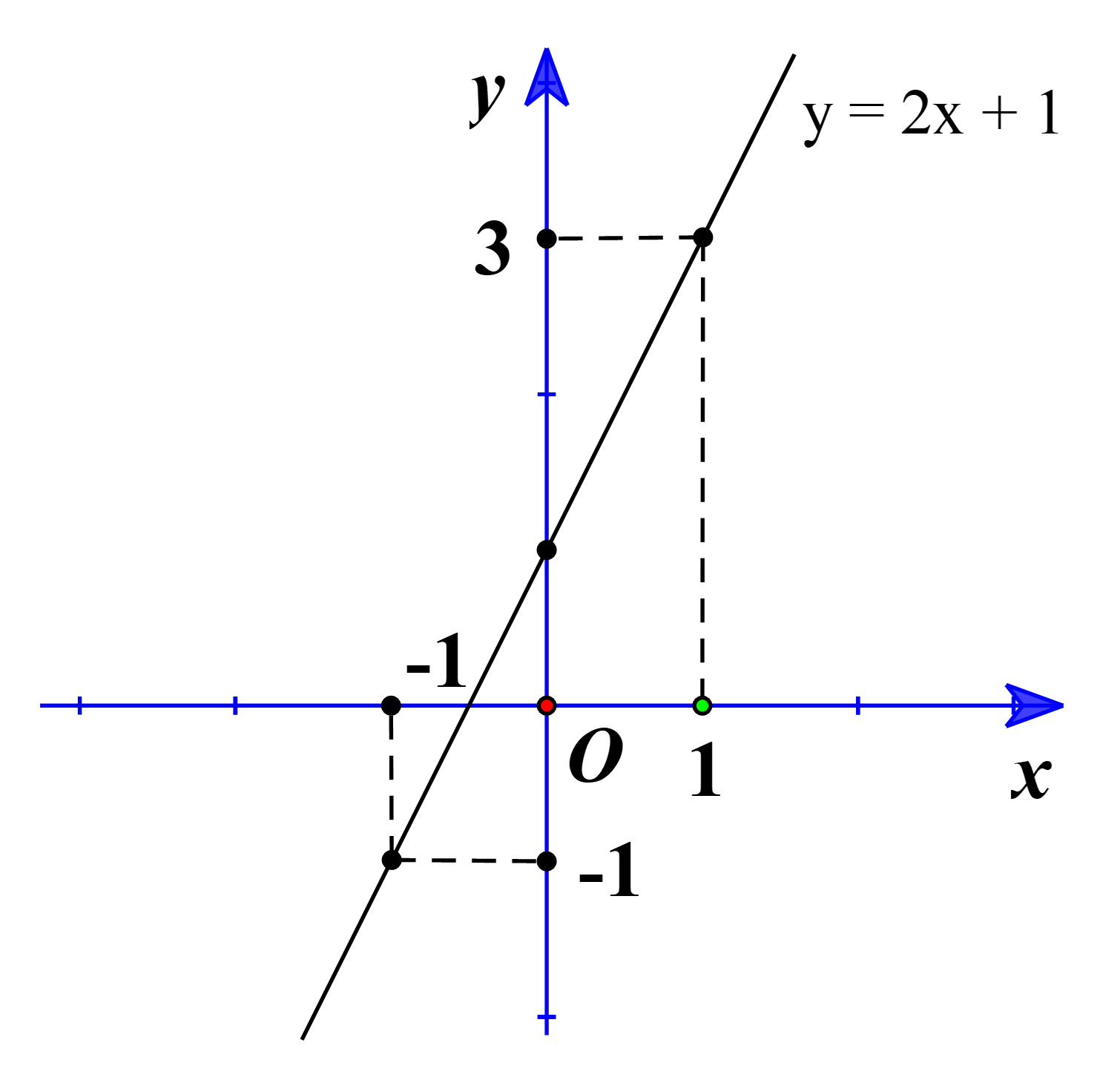
a) Khi m = 0 thì d có dạng y = 2x + 1
Bảng giá trị:
Ta có đường thẳng d đi qua hai điểm A(0; 1) và \({\rm{B}}\left( {\frac{{ - 1}}{2};0} \right)\)
b) Thay x = 2 vào y = 2x – 5 ta có
y = 2 . 2 – 5 = – 1
Thay x = 2, y = – 1 vào d ta có
– 1 = (2 – m). 2 + m + 1
⇔ – 1 = 4 – 2m + m + 1
⇔ m = 6 (thỏa mãn)
Khi m = 6 thì d có dạng y = – 4x + 7 cắt đường thẳng y = 2x – 5
Vậy m = 6 thì d cắt đường thẳng y = 2x – 5 tại điểm có hoành độ bẳng 2.
c) Vì m ≠ 2 nên d cắt Ox tại điểm \({\rm{C}}\left( {\frac{{m + 1}}{{m - 2}};0} \right)\) và cắt Oy tại điểm D(0; m + 1)
Ta có SCOD = \(\frac{1}{2}\left| {\frac{{m + 1}}{{m - 2}}} \right|\left| {m + 1} \right|\)= 2
⇔ (m + 1)2 = 4\(\left| {{\rm{m}} - 2} \right|\)
\( \Leftrightarrow \left[ \begin{array}{l}{\left( {m + 1} \right)^2} = 4(m - 2)\\{\left( {m + 1} \right)^2} = 4(2 - m)\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}{m^2} + 2m + 1 = 4m - 8\\{m^2} + 2m + 1 = 8 - 4m\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}{m^2} - 2m + 9 = 0\\{m^2} + 6m - 7 = 0\end{array} \right.\)
\( \Leftrightarrow \left[ \begin{array}{l}{m^2} - 2m + 9 = 0\\(m - 1)(m + 7) = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = 1\\m = - 7\end{array} \right.\)(thỏa mãn)
Vậy m = 1 hoặc m = – 7 thì d cùng với các trục tọa độ Ox, Oy tạo thành một tam giác có diện tích bẳng 2.

