Cho hàm số lôgarit y = log cơ số 2 của x

Hoạt động 5 trang 43 Toán 11 Tập 2: Cho hàm số lôgarit y = log₂x.

a) Tìm giá trị y tương ứng với giá trị x trong bảng sau:

b) Trong mặt phẳng tọa độ Oxy, biểu diễn điểm (x; y) trong bảng giá trị ở câu a. Bằng cách làm tương tự, lấy nhiều điểm (x; log₂x) với x ∈ (0; +∞) và nối lại, ta được đồ thị hàm số y = log₂x (Hình 6).

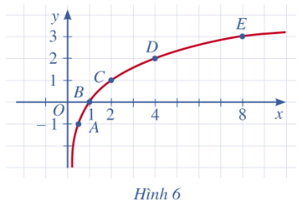
c)Cho biết tọa độ giao điểm đồ thị hàm số y = log₂x với trục hoành và vị trí của đồ thị hàm số đó so với trục tung.

d)Quan sát đồ thị hàm số y = log₂x, nêu nhận xét về:

• $\underset{x\to 0^{+}}{\lim }{\log }_{2}x,\underset{x\to +\infty }{\lim }{\log }_{2}x;$

• Sự biến thiên của hàm số y = log₂x và lập bảng biến thiên của hàm số đó.

Trả lời

a) Xét hàm số y = log₂x.

Thay x = 0,5 vào hàm số y = log₂x ta được y = log₂0,5 = y = log₂2⁻¹ = –1.

Tương tự, thay lần lượt các giá trị x = 1; x = 2; x = 4; x = 8 vào hàm số y = log₂x, ta được bảng sau:

b) Các điểm A(0,5; –1), B(1; 0), C(2; 1); D(4; 2) và E(8; 3) được biểu diễn trên mặt phẳng tọa độ Oxy như Hình 6.

Bằng cách làm tương tự, lấy nhiều điểm (x; log₂x) với x ∈ (0; +∞) và nối lại, ta được đồ thị hàm số y = log₂x (Hình 6).

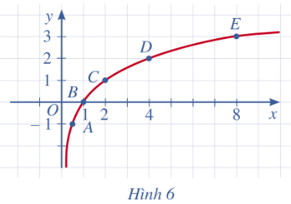
c) Giao điểm đồ thị hàm số y = log₂x với trục hoànhlà B(1; 0) và đồ thị hàm số y = log₂xnằm ở phía biên phải trục tung, đi lên kể từ trái sang phải.

d) Từ đồ thị ta thấy:

• $\underset{x\to 0^{+}}{\lim }{\log }_{2}x=-\infty ,\underset{x\to +\infty }{\lim }{\log }_{2}x=+\infty$

• Đồ thị hàm số y = log₂xđi lên kể từ trái sang phải (với x ∈ (0; +∞)) nên hàm số y = log₂xđồng biến trên (0; +∞).

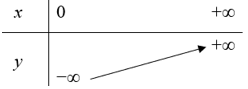
Bảng biến thiên của hàm số đó:

Xem thêm các bài giải SGK Toán lớp 11 Cánh diều hay, chi tiết khác: