Cho hàm số f(x) có đạo hàm f’(x) = x(x - 1)(x + 4)^3 , với mọi x thuộc R
Cho hàm số f(x) có đạo hàm f’(x) = x(x − 1)(x + 4)3 , ∀ x ∈ R. Số điểm cực tiểu của hàm số đã cho là
A. 2;
B. 3;
C. 4;
D. 1.
Đáp án đúng là: A
Ta có
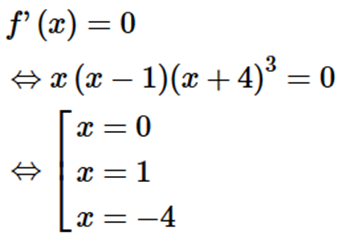
Ta có bảng xét dấu của f’(x)
Dựa vào bảng xét dấu của f'(x) suy ra hàm số đã cho có 2 điểm cực tiểu.
Vậy ta chọn đáp án A.