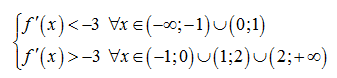Câu 48: Cho hàm số đa thức y = f(x) có đạo hàm trên ℝ, f(0) < 0 và đồ thị hình bên dưới là đồ thị của đạo hàm f’(x). Hỏi hàm số g(x) = |f(x) + 3x| có bao nhiêu điểm cực trị?
Đáp án đúng là: B
Xét hàm số h(x) = f(x) + 3x, x ∈ ℝ
h’(x) = f’(x) + 3, x ∈ R
h’(x) = 0 ⇔ f’(x) = – 3
⇔ x ∈ { – 1; 0; 1; 2}
Với x = 2 là nghiệm kép vì qua nghiệm x = 2 thì h’(x) không đổi dấu
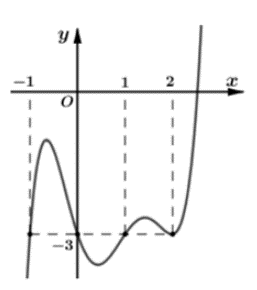
Dựa vào đồ thị của f’(x) ta có
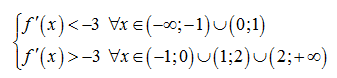
Mà h(0) = f(0) + 3 . 0 = f(0) < 0
Bảng biến thiên của hàm số h(x) = f(x) + 3x
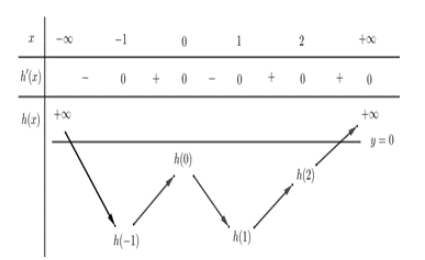
Từ đó suy ra bảng biến thiên của hàm số g(x) = | f(x) + 3x | = | h(x) |
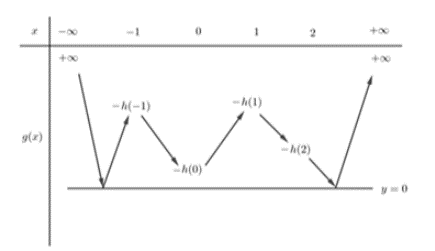
Từ bảng biến thiên ta thấy hàm số có 5 điểm cực trị
Vậy ta chọn đáp án B.