Cho hàm số bậc nhất \(y = \frac{3}{4}x + 3\) có đồ thị là đường thẳng (d).

a) Vẽ (d) trên mặt phẳng toạ độ Oxy.

b) Tính khoảng cách từ gốc toạ độ O đến đường thẳng (d).

Lời giải

a) Xét hàm số \(y = \frac{3}{4}x + 3\) (d).

• Giao điểm của d với trục tung là:

Với x = 0 ta có y = 3

Do đó d cắt trục tung tại điểm A(0; 3).

• Giao điểm của d với trục hoành là:

Với y = 0 ta có x = –4.

Do đó d cắt trục hoành tại điểm B(–4; 0).

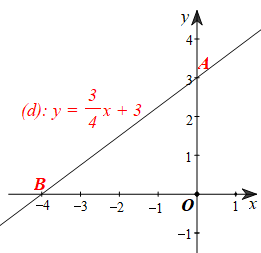
Vậy đồ thị hàm số đã cho là đường thẳng đi qua hai điểm A(0; 3) và B(–4; 0) (hình vẽ).

b) Kẻ OH ⊥ D, khi đó khoảng cách từ O đến đường thẳng d là độ dài đoạn thẳng OH.

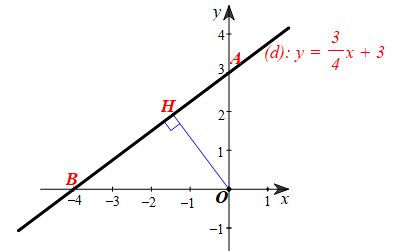
Ta có: A(0; 3) suy ra OA = 3;

           B(–4; 0) suy ra OB = 4.

Xét ∆OAB vuông tại O, theo hệ thức lượng trong tam giác vuông ta có:

\(\frac{1}{{O{H^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{O{B^2}}}\)

Do đó \(\frac{1}{{O{H^2}}} = \frac{1}{{{3^2}}} + \frac{1}{{{4^2}}} = \frac{{25}}{{144}}\)

Suy ra \(O{H^2} = \frac{{144}}{{25}}\) nên \(OH = \frac{{12}}{5} = 2,4\).