Luyện tập 3 trang 108 Toán 11 Tập 1: Cho hai mặt phẳng (P) và (Q) song song với nhau. Đường thẳng a cắt hai mặt phẳng trên theo thứ tự tại A, B. Đường thẳng b song song với đường thẳng a và cắt hai mặt phẳng (P) và (Q) lần lượt tại A’, B’. Chứng minh rằng AB = A’B’.
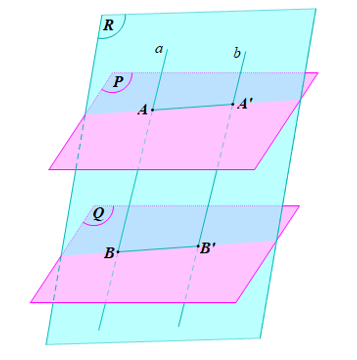
Giả sử (R) = (a, b).
Ta có: A ∈ (R) và A ∈ (P) nên A là giao điểm của hai mặt phẳng (R) và (P).
A’ ∈ (R) và A’ ∈ (P) nên A’ là giao điểm của hai mặt phẳng (R) và (P).
Do đó (R) ∩ (P) = AA’.
Tương tự ta cũng có (R) ∩ (Q) = BB’.
Do (P) // (Q);
(R) ∩ (P) = AA’;
(R) ∩ (Q) = BB’
Suy ra AA’ // BB’
Trong mp(R), xét tứ giác ABB’A’ có: AA’ // BB’ và AB // A’B’ (do a // b)
Suy ra ABB’A’ là hình bình hành
Do đó AB = A’B’.
Xem thêm các bài giải SGK Toán lớp 11 Cánh diều hay, chi tiết khác:
Bài 2: Hai đường thẳng song song trong không gian
Bài 3: Đường thẳng và mặt phẳng song song
Bài 4: Hai mặt phẳng song song
Bài 5: Hình lăng trụ và hình hộp
Bài 6: Phép chiếu song song. Hình biểu diễn của một hình không gian