Cho H, K là các giao điểm của đường tròn (O1), (O2). Đường thẳng O1H cắt (O1) tại A , (O2) tại B . O2H cắt (O1) tại C và (O1) tại D. Chứng minh rằng ba đường thẳng BC, BD, HK đồng quy tại 1 điểm.
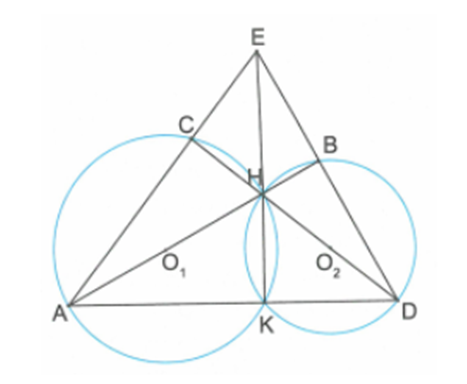
Gọi giao điểm của AC và BD là E
Các tam giác ACH, AKH nội tiếp đường tròn (O1) có cạnh HA là đường kính nên tam giác ACH vuông tại C, tam giác AHK vuông tại K
Suy ra \(\left\{ \begin{array}{l}DC \bot A{\rm{E (1)}}\\HK \bot AK{\rm{ (2)}}\end{array} \right.\)
Các tam giác HDK, HDB nội tiếp đường tròn (O2) có cạnh HD là đường kính nên tam giác HDK vuông tại K, tam giác HBD vuông tại B
Suy ra \(\left\{ \begin{array}{l}AB \bot D{\rm{E (4)}}\\HK \bot KD{\rm{ (3)}}\end{array} \right.\)
Từ (2) và (3) suy ra A, K, D thẳng hàng
Do đó HK ⊥ AD
Từ (1) và (4) suy ra H là trực tâm tam giác AED
Do đó HE ⊥ AD
Suy ra H thuộc EK
Vậy BC, BD, HK đồng quy tại 1 điểm.