Cho f(x) = −x^2 − 2(m − 1)x + 2m − 1. Tìm m để bất phương trình f(x) > 0 đúng với mọi x thuộc

Câu 1: Cho f(x) = −x² − 2(m − 1)x + 2m − 1.

Tìm m để bất phương trình f(x) > 0 đúng với mọi x thuộc (0; 1)

Trả lời

f(x) = −x^2 − 2(m − 1)x + 2m − 1

Xét ∆’ = (m − 1)2− (−1)(2m − 1) = m2 ≥ 0, ∀x ∈ℝ

• TH1: ∆’= 0 ⇒ m = 0

Khi đó f(x) = −x2 + 2x − 1 = −(x − 1)2 ≤ 0, ∀x ∈ℝ

Vậy với m = 0 không thỏa mãn yêu cầu bài toán

• TH2: ∆’ > 0 ⇒ m ≠ 0

Khi đó f(x) = 0 cho hai nghiệm a, b

Ta có BBT của f(x) = 0 như sau:

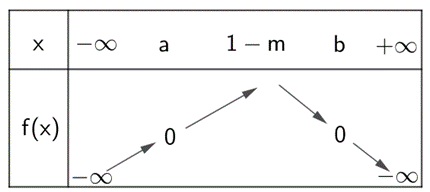
Để f(x) > 0 đúng với mọi x thuộc (0; 1) thì:

$\{\begin{array}{c}f\left(0\right)\le 0\\ f\left(1\right)\ge 0\end{array}\iff \{\begin{array}{c}2m-1\le 0\\ 0\ge 0\end{array}\iff m\le \frac{1}{2}$

$\frac{$ m\le \frac{1}{2}$}{}$