Cho đường tròn tâm O và điểm M nằm ngoài đường tròn. Qua M kẻ các tiếp tuyến MA, MB với đường tròn (A, B là các tiếp điểm). Đường thẳng d thay đổi đi qua M cắt đường tròn tại 2 điểm phân biệt
29
19/05/2024
Cho đường tròn tâm O và điểm M nằm ngoài đường tròn. Qua M kẻ các tiếp tuyến MA, MB với đường tròn (A, B là các tiếp điểm). Đường thẳng d thay đổi đi qua M cắt đường tròn tại 2 điểm phân biệt C và D (C nằm giữa M và D)
a) Chứng minh tứ giác AMBO nội tiếp
b) Chứng minh MA2 = MC.MD
c) Chứng minh đường tròn ngoại tiếp tam giác OCD luôn đi qua điểm cố định khác O
Trả lời
Lời giải
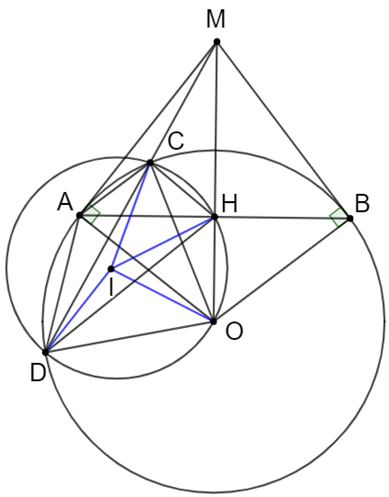
a) Xét tứ giác AOBM với \(\widehat {MAO}\) và \(\widehat {MBO}\) có:
\(\widehat {MAO} + \widehat {MBO} = 90^\circ + 90^\circ = 180^\circ \).
Do đó AOBM là tứ giác nội tiếp đường tròn.
b) Xét ∆MCA và ∆MAD có:
\(\widehat {MAC} = \widehat {MDA}\) (góc tạo bởi tia tiếp tuyến và dây cung, góc nội tiếp đường tròn cùng chắn cung AC)
\(\widehat M\) là góc chung
Þ ∆MCA ᔕ ∆MAD (g.g)
\( \Rightarrow \frac{{MC}}{{MA}} = \frac{{MA}}{{MD}} \Rightarrow M{A^2} = MC.MD\)
c) Lấy H là giao điểm của MO và AB.
Vì I là tâm đường tròn ngoại tiếp tam giác COD
Áp dụng hệ thức lượng trong tam giác vuông MAO vuông tại A có AH là đường cao nên suy ra MA2 = MH.MO.
Mà MA2 = MC.MD (cmt)
Þ MH.MO = MC.MD
\(\frac{{MH}}{{MD}} = \frac{{MC}}{{MO}}\)
Xét ∆MHD và ∆MCO có:
\(\frac{{MH}}{{MD}} = \frac{{MC}}{{MO}}\) (cmt)
\(\widehat M\): góc chung
Þ ∆MHD ᔕ ∆MCO (g.g)
\( \Rightarrow \widehat {MDH} = \widehat {MOC} \Rightarrow \widehat {CDH} = \widehat {HOC}\)
Þ Tứ giác CHOD nội tiếp đường tròn (Hai đỉnh kề nhau cùng nhìn một cạnh chứa hai đỉnh còn lại với hai góc bằng nhau).
Þ H thuộc đường tròn (I).
Vậy (I) đi qua điểm cố định H là giao của MO và AB; với A, B là hai tiếp điểm từ điểm M cố định đến đường tròn (O).

