Lời giải
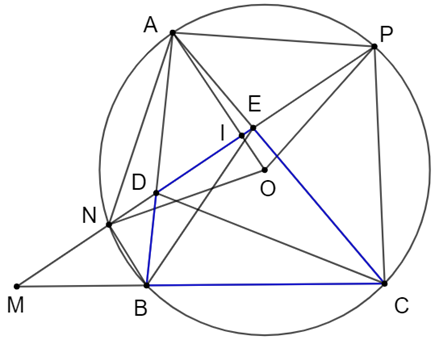
a) Gọi I là giao điểm của OA và NP
Ta có độ dài cung AN bằng độ dài cung AP nên suy ra AN = AP
Và ON = OP = R.
Þ OA là đường trung trực của đoạn thẳng NP
Þ OA ^ NP tại I
Þ \(\widehat {AID} = 90^\circ \Rightarrow \widehat {ADI} = 90^\circ - \widehat {IAD}\)
Hay \(\widehat {ADP} = 90^\circ - \widehat {OAB}\)
Lại có: OA = OB Þ ∆OAB cân tại O.
\( \Rightarrow \widehat {OAB} = \frac{{180^\circ - \widehat {AOB}}}{2} = 90^\circ - \frac{{\widehat {AOB}}}{2}\)
Suy ra \(\widehat {ADP} = 90^\circ - \left( {90^\circ - \frac{{\widehat {AOB}}}{2}} \right) = \frac{{\widehat {AOB}}}{2}\).
Mà \(\widehat {MDB} = \widehat {ADP}\) (Hai góc đối đỉnh) \( \Rightarrow \widehat {MDB} = \frac{{\widehat {AOB}}}{2}\).
Đường tròn (O) có: \(\widehat {ACB}\) là góc nội tiếp chắn cung AB và \(\widehat {AOB}\) là góc ở tâm chắn cung AB nên suy ra:
\(\widehat {ACB} = \frac{{\widehat {AOB}}}{2} \Rightarrow \widehat {ACB} = \widehat {MDB}\)
Hay \(\widehat {ECB} = \widehat {MDB}\).
Tứ giác BNDC có \[\widehat {ECB} + \widehat {EDB} = \widehat {MDB} + \widehat {EDB} = \widehat {MDE} = 180^\circ \].
Suy ra BNDC là tứ giác nội tiếp.
b) BNPC là tứ giác nội tiếp nên suy ra \(\widehat {NPC} + \widehat {NBC} = 180^\circ \).
Lại có \(\widehat {MBN} + \widehat {NBC} = \widehat {MBC} = 180^\circ \)
\( \Rightarrow \widehat {MBN} = \widehat {MPC}\)
Xét ∆MBN và ∆MPC có:
\(\widehat {MBN} = \widehat {MPC}\) (cmt)
\(\widehat M\): góc chung
Þ ∆MBN ᔕ ∆MPC (g.g).
\( \Rightarrow \frac{{MB}}{{MP}} = \frac{{MN}}{{MC}} \Rightarrow MB.MC = MN.MP\).

