Lời giải
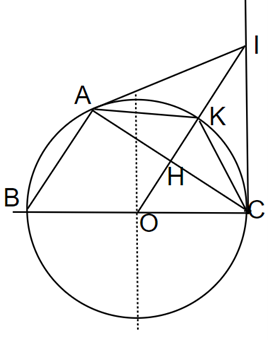
a) Ta có BC là đường kính của (O).
Mà A Î (O) nên ∆ABC nội tiếp đường tròn tâm O, đường kính BC.
Do đó ∆ABC vuông tại A.
b) Ta có ∆ABC vuông tại A nên AB ^ AC.
Mà AB // OK (gt) suy ra AC ^ OK.
Mà OI cắt AC tại H nên OH ^ AC.
Xét ∆OAC có OA = OC và H là đường cao.
Suy ra ∆OAC là tam giác cân tại O có OH là tia phân giác.
Do đó \(\widehat {AOH} = \widehat {HOC}\).
Xét ∆AOI và ∆COI có:
OA = OC
OI: cạnh chung
\(\widehat {AOH} = \widehat {HOC}\)
Do đó ∆AOI = ∆COI (c.g.c)
Suy ra \(\widehat {OAI} = \widehat {OCI}\) (hai cạnh tương ứng).
Mà \(\widehat {OCI} = 90^\circ \) (Do IC là tiếp tuyến của (O) tại C)
\( \Rightarrow \widehat {OAI} = 90^\circ \)
Þ OA ^ AI tại A
Þ IA là tiếp tuyến của (O) tại A
c) \(OC = \frac{{BC}}{2} = 15\;\left( {cm} \right)\)
• \(AC = \sqrt {B{C^2} - A{B^2}} = \sqrt {{{30}^2} - {{18}^2}} = 24\;\,\left( {cm} \right)\)
\( \Rightarrow HC = \frac{{AC}}{2} = 12\;cm\)
• \(OH = \sqrt {O{C^2} - H{C^2}} = \sqrt {{{15}^2} - {{12}^2}} = 9\;cm\)
• \(\cos \widehat {HOC} = \frac{{OH}}{{OC}} = \frac{9}{{15}} = \frac{3}{5} = \cos \widehat {IOC}\)
\( \Rightarrow \cos \widehat {IOC} = \frac{{OC}}{{OI}} = \frac{3}{5}\)
\( \Rightarrow OI = OC:\frac{3}{5} = 15:\frac{3}{5} = 25\;(cm)\)
• \(CI = \sqrt {O{I^2} - O{C^2}} = \sqrt {{{25}^2} - {{15}^2}} = 20\;\,(cm)\).
Vậy OI = 25 cm; CI = 20 cm.

