Cho đường tròn tâm O bán kính R và một đường thẳng d cố định không giao nhau

Đề bài: Cho đường tròn tâm O bán kính R và một đường thẳng d cố định không giao nhau. Hạ OH vuông góc với d. M là một điểm tùy ý trên d (M không trùng với H). Từ M kẻ hai tiếp tuyến MP và MQ với đường tròn (O; R) (P, Q là các tiếp điểm và tia MQ nằm giữa hai tia MH và MO). Dây cung PQ cắt OH và OM lần lượt tại I và K.

1) Chứng minh rằng tứ giác OMHQ nội tiếp.

2) Chứng minh rằng $\widehat{OMH}=\widehat{OIP}$

3) Chứng minh rằng khi M di chuyển trên đường thẳng d thì điểm I luôn cố định.

4) Biết $OH=R\sqrt{2}$ , tính IP . IQ.

Trả lời

Hướng dẫn giải:

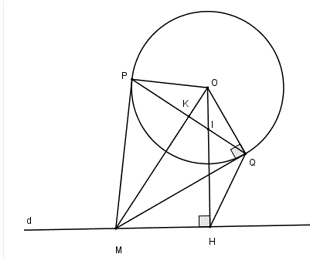
1) Xét tứ giác OMHQ có $\widehat{OQM}={90}^0$ (MQ là tiếp tuyến của (O))

                                        $\widehat{OHM}={90}^0$ ( $OH\perp d$ )

Vậy tứ giác OMHQ nội tiếp (Tứ giác có hai góc nội tiếp bằng nhau)

2) Ta có: $\widehat{OMH}+\widehat{MOH}={90}^0$ (tổng hai góc nhọn trong tam giác vuông OMH)

Ta có   OP = OQ = R, MP = MQ (tính chất hai tiếp tuyến cắt nhau)

→ OM là trung trực của PQ $\to OM\perp PQ$

$\to \widehat{OIP}+\widehat{MOH}={90}^0$ (tổng hai góc nhọn trong tam giác vuông OIK)

Vậy $\widehat{OMH}=\widehat{OIP}$ (cùng phụ với $\widehat{MOH}$ )

3) Xét hai tam giác OIK và OMH có  $\widehat{OMH}=\widehat{OIP}$ (cmt), $\widehat{OHM}=\widehat{OKI}={90}^0$

Suy ra  $\Delta OIK~\Delta OMH$ (g.g)

$\to \frac{OI}{OM}=\frac{OK}{OH}\to OI=\frac{OK.OM}{OH}$

Áp dụng hệ thức lượng trong tam giác vuông OQM có $R^2=O{Q}^2=OK.OM$

$\to OI=\frac{R^2}{OH}$

Vì d cố định nên OH không đổi, R luôn không đổi nên OI không đổi. Mà $I\in OH$ cố định nên I cố định.

4) Xét tứ giác OPMQ có: 

$\widehat{OPM}+\widehat{OQM}={180}^0\to$ Tứ giác OPMQ nội tiếp (Tứ giác có tổng hai góc đối bằng ${180}^0$ )

$\to \widehat{OPI}=\widehat{OMQ}$ (hai góc nội tiếp cùng chắn cung OQ)