Cho đường tròn (O) đường kính AB. Vẽ tiếp tuyến Ax, với đường tròn (O) (A là tiếp điểm ). Qua C thuộc tia Ax, vẽ đường thẳng
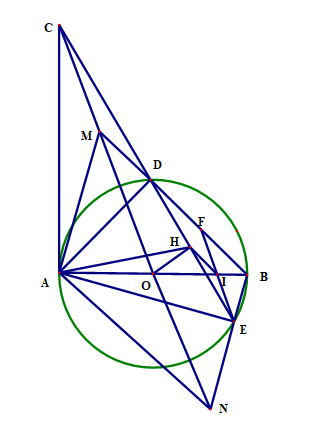
Cho đường tròn (O) đường kính AB. Vẽ tiếp tuyến Ax, với đường tròn (O) (A là tiếp điểm ). Qua C thuộc tia Ax, vẽ đường thẳng cắt đường tròn (O) tại hai điểm D và E (D nằm giữa C và E; D và E nằm về hai phía của đường thẳng AB). Từ O vẽ OH vuông góc với đoạn thẳng DE tại H.
a) Chứng minh : tứ giác AOHC nội tiếp.
b) Chứng minh : AC . AE = AD . CE
c) Đường thẳng CO cắt tia BD, tia BE lần lượt tại M và N. Chứng minh : AM // BN