Lời giải
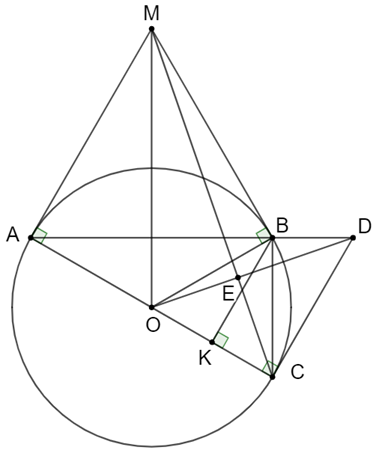
a) Xét tứ giác AOBM có: \(\widehat {MAO} + \widehat {MBO} = 90^\circ + 90^\circ = 180^\circ \)
Þ AOBM là tứ giác nội tiếp đường tròn.
Vậy bốn điểm A, B, M, O cùng thuộc một đường tròn.
b) Theo tính chất 2 tiếp tuyến cắt nhau, ta có:
MA và MB là 2 tiếp tuyến cắt nhau tại M Þ MA = MB.
Lại có OA = OB = R
Þ OM là đường trung trực của đoạn thẳng AB
Þ OM ^ AB (1)
Mà \[\widehat {ABC} = 90^\circ \] (Do góc nội tiếp chắn nửa đường tròn)
Þ AB ^ BC (2)
Từ (1) và (2) Þ OM // BC
c) Do OM // BC \( \Rightarrow \widehat {AOM} = \widehat {ACB}\) (Hai góc ở vị trí đồng vị)
Þ \(\widehat {AOM} = \widehat {KCB}\)
Lại có OM là đường trung trực trong tam giác cân OAB nên nó cũng là đường phân giác của tam giác OAB
\( \Rightarrow \widehat {AOM} = \widehat {BOM}\)
Nên suy ra \(\widehat {KCB} = \widehat {BOM}\)
Xét ∆BCK và ∆MOB có:
\(\widehat {KCB} = \widehat {BOM}\) (cmt)
\(\widehat {BKC} = \widehat {MBO}\;\left( { = 90^\circ } \right)\)
Þ ∆BCK ᔕ ∆MOB (g.g)
\( \Rightarrow \frac{{CK}}{{OB}} = \frac{{CB}}{{OM}} \Rightarrow CK.OM = OB.CB\) (đpcm)
d) Lấy E là giao điểm của CM và OD.
Ta có: \(\widehat {BCD} = \widehat {BAC}\) (Hai góc cùng phụ với \(\widehat {BCA}\))
Mà \(\widehat {BMO} = \widehat {BAO}\) (Hai góc nội tiếp cùng chắn cung BO)
\( \Rightarrow \widehat {BMO} = \widehat {BCD}\)
Xét ∆BMO và ∆BCD có:
\(\widehat {BMO} = \widehat {BCD}\) (cmt)
\(\widehat {MBO} = \widehat {CBD}\;\left( { = 90^\circ } \right)\)
Þ ∆BMO ᔕ ∆BCD (g.g)
\( \Rightarrow \frac{{BM}}{{BC}} = \frac{{BO}}{{BD}}\)
Mà \(\widehat {MBC} = \widehat {OBD}\)
Þ ∆MBC ᔕ ∆OBD (c.g.c)
\( \Rightarrow \widehat {BMC} = \widehat {BOD}\)
Þ Tứ giác BMOE nội tiếp đường tròn
\( \Rightarrow \widehat {MEO} = \widehat {MBO} = 90^\circ \) (Hai góc nôij tiếp cùng chắn cung MO)
Þ OD ^ CM (đpcm).

