Cho đường tròn (O) và điểm A nằm ngoài đường tròn. Kẻ các tiếp tuyến AB, AC và cát
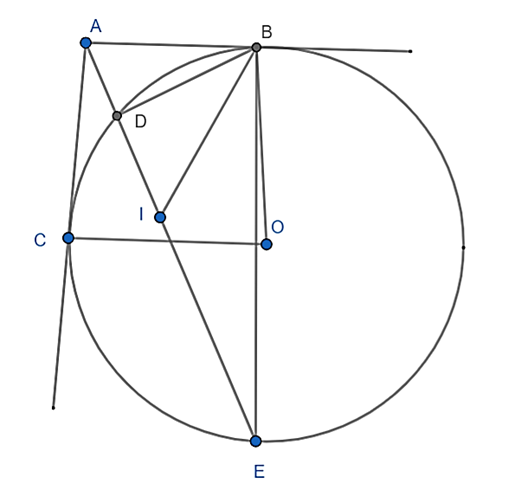
Cho đường tròn (O) và điểm A nằm ngoài đường tròn. Kẻ các tiếp tuyến AB, AC và cát tuyến ADE với đường tròn (D nằm giữa A và E). Tia phân giác góc \(\widehat {DBE}\)cắt DE tại I. Chứng minh rằng:
a) \(\frac{{BD}}{{BE}} = \frac{{AD}}{{AB}}\).
b) \(\frac{{BD}}{{BE}} = \frac{{CD}}{{CE}}\).