Cho đường tròn (O; R) và dây MN. Các tiếp tuyến của (O) tại M, N cắt nhau ở A. Qua M, kẻ đường thẳng song song với AN, cắt (O) tại điểm thứ hai là P. Q là giao điểm của AP và (O), K là giao điểm của MQ và AN. Chứng minh

a) AK² = KQ.KM.

b) K là trung điểm của AN.

Lời giải

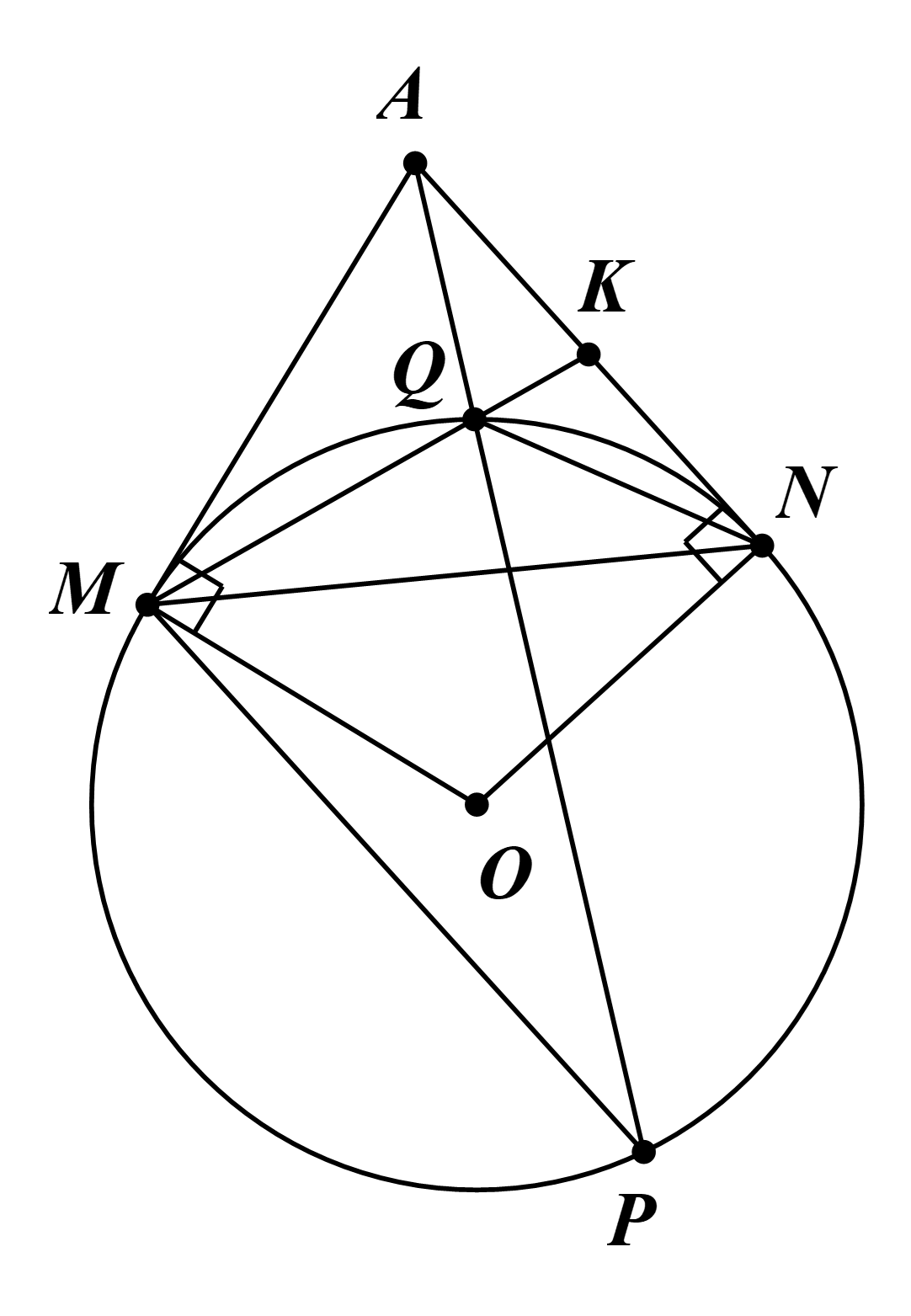
a) Ta có \(\widehat {AMQ} = \widehat {MPQ}\) (góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn một cung) và \(\widehat {QAK} = \widehat {MPQ}\) (do AK // MP).

Suy ra \(\widehat {AMQ} = \widehat {QAK}\).

Xét ∆AKQ và ∆MAK, có:

\(\widehat {AMQ} = \widehat {QAK}\) (chứng minh trên);

\(\widehat {AKQ}\) chung.

Do đó (g.g).

Suy ra \(\frac{{AK}}{{MA}} = \frac{{KQ}}{{AK}} = \frac{{AQ}}{{MK}}\).

\[ \Leftrightarrow \frac{{AK}}{{MA}} = \frac{{MK}}{{AK}} = \frac{{AQ}}{{KQ}}\]

\[ \Leftrightarrow \frac{{AK}}{{MK}} = \frac{{MA}}{{AK}} = \frac{{AQ}}{{KQ}}\]

\[ \Leftrightarrow \frac{{AK}}{{MK}} = \frac{{KQ}}{{AK}} = \frac{{AQ}}{{MA}}\].

Vậy AK² = KQ.KM (điều phải chứng minh).

b) Xét ∆KQN và ∆KNM, có:

\(\widehat {KNQ} = \widehat {KMN}\) (góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn một cung);

\(\widehat {MKN}\) chung.

Do đó (g.g).

Suy ra \(\frac{{KQ}}{{KN}} = \frac{{QN}}{{NM}} = \frac{{KN}}{{KM}}\).

Do đó KN² = KQ.KM.

Mà AK² = KQ.KM (câu a).

Suy ra KN = AK.

Vậy K là trung điểm AN.