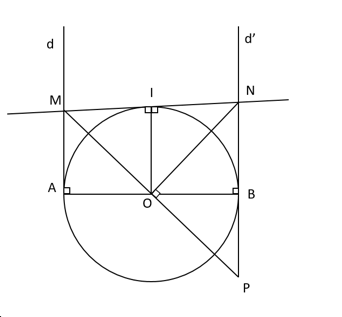
Cho đường tròn (O; R), đường kính AB. Qua A và B vẽ lần lượt hai tiếp tuyến (d) và (d’) với đường tròn (O). Một đường thẳng qua O cắt đường thẳng (d) ở M và cắt đường thẳng (d’) ở P. Từ O vẽ một tia vuông góc với MP và cắt (d’) ở N.

a) Chứng minh OM = OP và ∆NMP cân.

a)

Xét ∆AMO và ∆BPO có:

OA = OB = R

$\widehat{AOM}=\widehat{BOP}$ (đối đỉnh)

$\widehat{MAO}=\widehat{PBO}={90}^o$

⇒ ∆AMO = ∆BPO (gcg)

⇒ OM = OP ⇒ O là trung điểm MP.

Xét ∆MNP có NO vừa là đường cao vừa là đường trung tuyến

⇒ ∆MNP cân tại N.