Cho đường tròn (O; R), dây AB khác đường kính. Vẽ về hai phía của AB

Đề bài: Cho đường tròn (O; R), dây AB khác đường kính. Vẽ về hai phía của AB các dây AC, AD. Gọi H và K theo thứ tự là chân các đường vuông góc kẻ từ B đến AC và AD. Chứng minh rằng:

a) Bốn điểm A, H, B, K thuộc cùng một đường tròn;

b) HK < 2R.

Trả lời

Hướng dẫn giải:

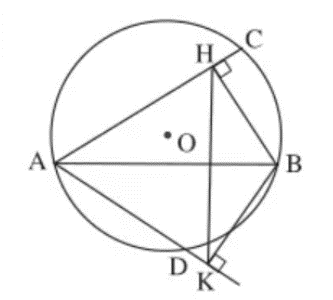
a)

Xét tam giác AHB vuông tại H

Có:  $\widehat{AHB}=90°$

Do đó, tam giác AHB nội tiếp đường tròn đường kính AB.

Hay A, H, B nằm trên đường tròn đường kính AB (1)

Xét tam giác AKB vuông tại K có:

$\widehat{AKB}=90°$

Do đó, tam giác AKB nội tiếp đường tròn đường kính AB

Hay A, K, B nằm trên đường tròn đường kính AB (2)

Từ (1) và (2) ta có bốn điểm A, H, K, B cùng nằm trên đường tròn đường kính AB.

b)

Xét đường tròn đường kính AB

Gọi I là trung điểm của AB

Ta có HK là dây cung không đi qua I 

⇒ HK < AB (1)

Xét đường tròn (O; R) có:

AB là dây cung không đi qua tâm O

⇒  AB < 2R (2)

Từ (1) và (2) ta suy ra HK < 2R