Lời giải

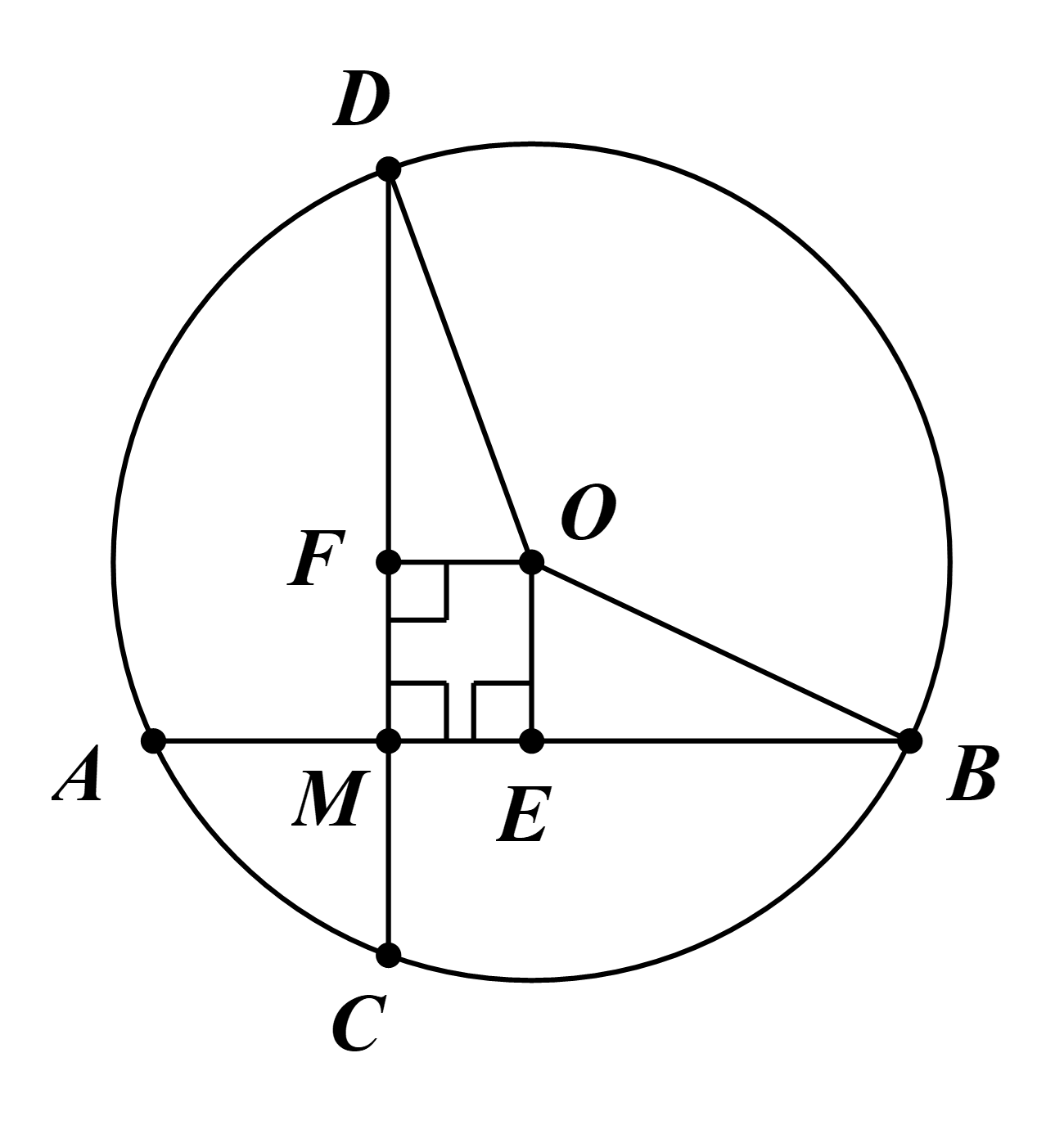
Lấy E, F lần lượt là trung điểm của hai dây AB, CD.

Khi đó OE ⊥ AB và OF ⊥ CD (quan hệ giữa đường kính và dây cung).

Mà FM ⊥ ME (giả thiết).

Suy ra tứ giác OEMF là hình chữ nhật.

Do đó OE = MF = CF – MC = \(\frac{{CD}}{2} - MC = \frac{{12}}{2} - 2 = 4\) (cm).

Ta có \(AE = \frac{{AB}}{2} = \frac{{14}}{2} = 7\) (cm).

Tam giác OEA vuông tại E: \(OA = \sqrt {O{E^2} + A{E^2}} = \sqrt {{4^2} + {7^2}} = \sqrt {65} \).

Suy ra \(R = OD = OA = \sqrt {65} \).

Tam giác ODF vuông tại F:

\[OF = \sqrt {O{D^2} - D{F^2}} = \sqrt {O{D^2} - {{\left( {\frac{{CD}}{2}} \right)}^2}} = \sqrt {{{\left( {\sqrt {65} } \right)}^2} - {{\left( {\frac{{12}}{2}} \right)}^2}} = \sqrt {29} \].

Vậy \(R = \sqrt {65} \) và khoảng cách từ tâm O đến dây CD bằng \(\sqrt {29} \).