Lời giải
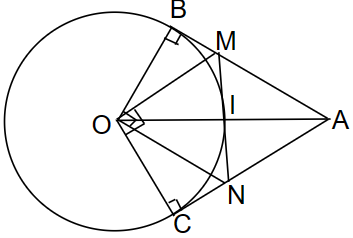
a) Xét (O;R) có EA , EC là 2 tiếp tuyến cắt nhau tại E
Suy ra AE = EC
Mà AO = OC nên EO là trung trực của AC
Hay EO ⊥ AC
Xét (O;R) có FC , FB là 2 tiếp tuyến cắt nhau tại F
Suy ra FB = FC
Mà OF = OB nên FO là trung trực của BC
Hay OF ⊥ BC
Ta có EF = EC + CF = AE+ BF
Vậy EF= AE+ BF
b) Vì tam giác ABC nội tiếp đường tròn đường kính AB
nên tam giác ABC vuông tại C
Suy ra AC ⊥ BD
Xét tam giác ABD vuông tại A có AC ⊥ BD
Suy ra AD2 = DC. DB (hệ thức lượng trong tam giác)
Vậy AD2 = DC. DB
c) Ta có EA = EC, OA = OC
Nên OE là trung trực của AC
Suy ra OE ⊥ AC
Mà AC ⊥ BD
Do đó OE // BD (quan hệ từ vuông góc đến song song)
Trên tia đối của tia EO lấy P sao cho EP = EH
Xét tứ giác AHDP có E là giao điêm của hai đường chéo AD và HP, E là trung điểm của HP
Suy ra AHDP là hình bình hành
Suy ra HI // PD
Do đó \(\frac{{{\rm{OI}}}}{{{\rm{DI}}}} = \frac{{{\rm{OH}}}}{{{\rm{PH}}}}\)
Vì HK // AP nên \(\frac{{{\rm{OK}}}}{{{\rm{AK}}}} = \frac{{{\rm{OH}}}}{{{\rm{PH}}}}\)
Mà \(\frac{{{\rm{OI}}}}{{{\rm{DI}}}} = \frac{{{\rm{OH}}}}{{{\rm{PH}}}}\)
Suy ra \(\frac{{{\rm{OI}}}}{{{\rm{DI}}}} = \frac{{{\rm{OK}}}}{{{\rm{AK}}}}\)
Do đó IK // AD.
d) Ta có IK // AD, AD ⊥ BA nên IK ⊥ AB
Xét tam giác IAO có HO ⊥ AC, IK ⊥ AO và OH cắt IK tại M
Suy ra M là trực tâm tam giác OIA
Do đó AM ⊥ IO (1)
Gọi Q là giao điểm của FO và AD
Xét tam giác OBF và tam giác OAQ có
\(\widehat {OBF} = \widehat {OAQ}\left( { = 90^\circ } \right)\)
OA = OB
\(\widehat {BOF} = \widehat {QOA}\) (hai góc đối đỉnh)
Do đó DOBF = DOAQ (g.c.g)
Suy ra FO = QO (hai cạnh tương ứng)
Xét tứ giác AFBQ có
AB cắt QF tại điểm O
O là trung điểm của AB, QF
Suy ra AFBQ là hình bình hành
Do đó AF // BQ
Xét tam giác BQD có AB ⊥ DQ, QF ⊥ DB
AB cắt QF tại O
Suy ra O là trực tâm tam giác BQD
Nên DO ⊥ QB
Mà BQ // AF (chứng minh trên)
Suy ra DO ⊥ AF (2)
Từ (1) và (2) suy ra A, M, F thẳng hàng
Vậy A, M, F thẳng hàng.

