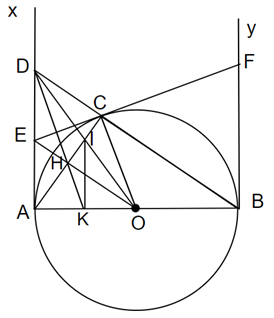
Cho đường tròn (O; R) có đường kính AB. Vẽ các tiếp tuyến Ax, By của đường
Cho đường tròn (O; R) có đường kính AB. Vẽ các tiếp tuyến Ax, By của đường tròn (O), trên đường trong (O) lấy 1 điểm C sao cho AC < BC. Tiếp tuyến tại C của đường tròn (O) cắt Ax, By lần lượt tại E và F.
a. Chứng minh EF = AE + BF
c. BC cắt Ax tại D. Chứng minh \(A{D^2} = DC.DB\)